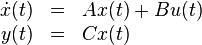Convection Reaction

Note: This page has not been verified by our editors.

This is a stub. Please expand.

Description

This benchmark models a chemical reaction by a convection-reaction partial differential equation. More details can be found in , , and , .

Origin

This benchmark is part of the SLICOT Benchmark Examples for Model Reduction.

Data

The system matrices $A$, $B$, $C$ are available from the SLICOT benchmarks page: pde.zip and are stored as MATLAB .mat file.

Dimensions

System structure:

$\begin{array}{rcl} \dot{x}(t) &=& Ax(t) + Bu(t) \\ y(t) &=& Cx(t) \end{array}$

System dimensions:

$A \in \mathbb{R}^{84 \times 84}$, $B \in \mathbb{R}^{84 \times 1}$, $C \in \mathbb{R}^{1 \times 84}$.

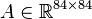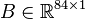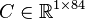Citation

To cite this benchmark, use the following references:

• For the benchmark itself and its data:

Niconet e.V., SLICOT - Subroutine Library in Systems and Control Theory, http://www.slicot.org

@MANUAL{slicot_pde,
 title =        {{SLICOT} - Subroutine Library in Systems and Control Theory},
 organization = {Niconet e.V.},
 address =      {\url{http://www.slicot.org}},
 key =          {SLICOT}
}

• For the background on the benchmark:

@ARTICLE{Saa88,
 author =       {Y. Saad},
 title =        {Projection and deflation method for partial pole assignment in linear state feedback},
 journal =      {IEEE Transactions on Automatic Control},
 volume =       {33},
 number =       {3},
 pages =        {290--297},
 year =         {1988},
 doi =          {10.1109/9.406}
}