Description
The method introduced here is described in [1] and [2], which is an extension of the Moment-matching method for nonparametric systems (see [3], [4] for moment-matching MOR). The method is applicable for linear parametrized systems, either in frequency domain or in time domain. For example, the parametric system in frequency domain:
where 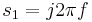 is the frequency domain variable,
is the frequency domain variable, 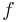 is the frequency.
is the frequency. 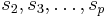 are the parameters of the system. They can be any scalar functions of some source parameters, like
are the parameters of the system. They can be any scalar functions of some source parameters, like 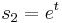 , where
, where 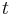 is time, or combinations of several physical (geometrical) parameters like
is time, or combinations of several physical (geometrical) parameters like 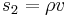 , where
, where  and
and  are two independent physical (geometrical) parameters.
are two independent physical (geometrical) parameters. 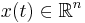 is the state vector,
is the state vector, 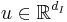 and
and 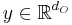 are the inputs and outputs of the
system, respectively.
are the inputs and outputs of the
system, respectively.
To obtain the reduced model in (2), a projection matrix
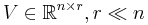 has to be computed.
has to be computed.
The matrix  is derived by orthogonalizing a number of moment
matrices of the system in (1) as follows, see [1] or [2].
is derived by orthogonalizing a number of moment
matrices of the system in (1) as follows, see [1] or [2].
By defining 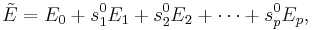 and
and 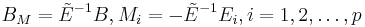 ,
we can expand
,
we can expand  in (1) at
in (1) at 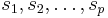 around
around ![p_0=[s_1^0,s_2^0,\cdots,s_p^0]](/morwiki/images/math/4/1/3/413a7d9006408a35467750f81e49d248.png) as below,
as below,
Here 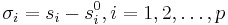 . We call the coefficients
in the above series expansion moment matrices of the parametrized
system, i.e.
. We call the coefficients
in the above series expansion moment matrices of the parametrized
system, i.e. 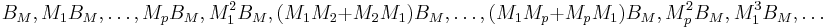 . The corresponding moments of the transfer function are those moment
matrices multiplied by
. The corresponding moments of the transfer function are those moment
matrices multiplied by  from the left. The matrix
from the left. The matrix  can be
generated by first explicitly computing some of the moment matrices
and then orthogonalizing them as suggested in [1].
The resulting
can be
generated by first explicitly computing some of the moment matrices
and then orthogonalizing them as suggested in [1].
The resulting  is desired to expand the subspace:
is desired to expand the subspace:
However,  does not really span the whole subspace, because the
latterly computed vectors in the subspace become linearly dependent
due to numerical instability. Therefore, with this matrix
does not really span the whole subspace, because the
latterly computed vectors in the subspace become linearly dependent
due to numerical instability. Therefore, with this matrix  one
cannot get an accurate reduced model which matches all the moments
algebraically included in the subspace.
one
cannot get an accurate reduced model which matches all the moments
algebraically included in the subspace.
Instead of directly computing the moment matrices in (3), a
numerically robust method is proposed in [2] ( the
detailed algorithm is described in [5] ), which combines
the recursion in (5) with the modified Gram-Schmidt
process to implicitly compute the moment matrices. The computed  is actually an orthonormal basis of the subspace as below,
is actually an orthonormal basis of the subspace as below,
Due to the numerical stability properties of
the repeated modified Gram-Schmidt process employed in
[2] and [5], the reduced model derived from  in (4) is computed in a numerically stable and accurate way. Applications of the method in [2], [5] to the parametric models Gyroscope, Silicon nitride membrane, and Microthruster Unit, can be found in [6].
in (4) is computed in a numerically stable and accurate way. Applications of the method in [2], [5] to the parametric models Gyroscope, Silicon nitride membrane, and Microthruster Unit, can be found in [6].
References
- ↑ 1.0 1.1 1.2 L. Daniel, O. C. Siong, L. S. Chay, K. H. Lee, and J.~White. "A multiparameter moment-matching model-reduction approach for generating geometrically parameterized interconnect performance models", IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst, 22(5): 678--693, 2004.
- ↑ 2.0 2.1 2.2 2.3 2.4 L. Feng and P. Benner, "A Robust Algorithm for Parametric Model Order Reduction", In Proc. Applied Mathematics and Mechanics (ICIAM 2007), 7(1): 10215.01--02, 2007.
- ↑ L. Feng, P. Benner, and J.G Korvink, "System-level modeling of MEMS by means of model order reduction (mathematical approximation)--mathematical background". In T. Bechtold, G. Schrag, and L. Feng, editors, System-Level Modeling of MEMS, Advanced Micro & Nanosystems. ISBN 978-3-527-31903-9, Wiley-VCH, 2013.
- ↑ A. Odabasioglu, M. Celik, and L. T. Pileggi, "PRIMA: passive reduced-order interconnect macromodeling algorithm", IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst.,17(8):645--654,1998.
- ↑ 5.0 5.1 5.2 L. Feng and P. Benner, "A robust algorithm for parametric model order reduction based on implicit moment matching", submitted.
- ↑ L. Feng, P. Benner, J.G Korvink, "Subspace recycling accelerates the parametric macromodeling of MEMS", International Journal for Numerical Methods in Engineering, 94(1): 84-110, 2013.

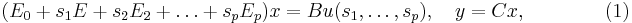


![x=[I-(\sigma_1M_1+\ldots +\sigma_pM_p)]^{-1}B_Mu(s_1,\ldots,s_p)
=\sum\limits_{i=0}^{\infty}(\sigma_1M_1+\ldots+\sigma_pM_p)^iB_Mu(s_1,\ldots,s_p).](/morwiki/images/math/c/5/7/c579a1cef93ab288b4390ee4162429bd.png)
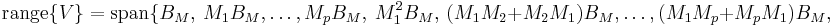
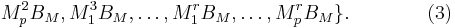
![R_0 =[B_M],](/morwiki/images/math/b/0/8/b082a405906483d3f30b5eabee73df9e.png)
![R_1=[M_1R_0,\ldots, M_pR_0],](/morwiki/images/math/c/c/d/ccd82b40f093fbee48c43629cfd7d6f1.png)
![R_2=[M_1R_1,\ldots, M_pR_1], \quad \quad \quad \quad (5)](/morwiki/images/math/4/6/f/46f9d6d092782aedbbb5c0414913612c.png)
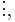
![R_r=[M_1R_{r-1},\ldots, M_pR_{r-1}]](/morwiki/images/math/5/7/8/5785ef8a934c9871a62b3d896e9ccd48.png)
