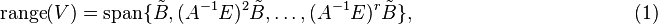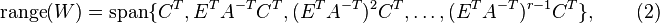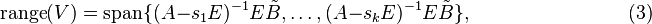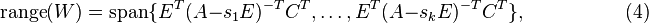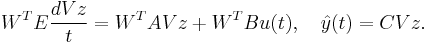Description
The moment-matching methods are also called the Krylov subspace methods[1], as well as Padé approximation methods[2]. They belong to the Projection based MOR methods. These methods are applicable to non-parametric linear time invariant systems, often descriptor systems, e.g.
They are very efficient in many engineering applications, such as circuit simulation, Microelectromechanical systems (MEMS) simulation, etc..
The basic steps are as follows. First, the transfer function
is expanded into a power series at an expansion point 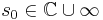 .
.
Let 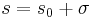 , then, within the convergence radius of the series, we have
, then, within the convergence radius of the series, we have
where 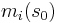 are called the moments of the transfer function about
are called the moments of the transfer function about 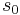 for
for 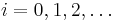 .
If the expansion point is chosen as zero, then the moments simplify to
.
If the expansion point is chosen as zero, then the moments simplify to 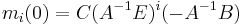 .
.
The goal in moment-matching model reduction is the construction of a reduced order
system where some moments 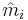 of the associated transfer function
of the associated transfer function 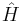 match some moments
of the original transfer function
match some moments
of the original transfer function  .
.
The matrices  and
and 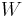 for model order reduction can be computed
from the vectors which are associated with the moments, for
example, using a single expansion point
for model order reduction can be computed
from the vectors which are associated with the moments, for
example, using a single expansion point 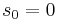 , by
, by
where 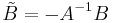 .
.
The transfer function 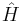 of the reduced model has good approximation properties around
of the reduced model has good approximation properties around 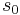 , which matches the first
, which matches the first 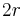 moments of
moments of 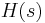 at
at 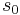 .
.
Using a set of 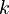 distinct expansion points
distinct expansion points  , the reduced model obtained by, e.g.,
, the reduced model obtained by, e.g.,
matches the first two moments at each 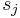 ,
, 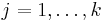 , see [3]. The reduced model is in the form as below
, see [3]. The reduced model is in the form as below
For the case of one expansion point in (1)(2), it can be seen that the columns of  ,
, 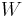 span Krylov subspaces
which can easily be computed by Arnoldi or Lanczos methods. The matrices
span Krylov subspaces
which can easily be computed by Arnoldi or Lanczos methods. The matrices  and
and 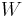 in (3)(4) can be computed with the rational Krylov algorithm in[3] or with the modified Gram-Schmidt process. In these algorithms only a few number of linear systems need to be solved, where matrix-vector multiplications are only used if using iterative solvers, which are simple to implement and the complexity of the resulting
methods is roughly
in (3)(4) can be computed with the rational Krylov algorithm in[3] or with the modified Gram-Schmidt process. In these algorithms only a few number of linear systems need to be solved, where matrix-vector multiplications are only used if using iterative solvers, which are simple to implement and the complexity of the resulting
methods is roughly 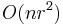 for sparse matrices
for sparse matrices 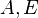 .
.
References
- ↑ R.W. Freund, "Model reduction methods based on Krylov subspaces". Acta Numerica, 12:267-319, 2003.
- ↑ P. Feldmann and R.W. Freund, "Efficient linear circuit analysis by Pade approximation via the Lanczos process". IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst., 14:639-649, 1995.
- ↑ 3.0 3.1 E.J. Grimme, "Krylov projection methods for model reduction. PhD thesis, Univ. Illinois, Urbana-Champaign, 1997.

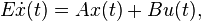
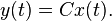
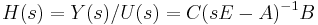
![H(s_0 + \sigma)= C[(s_{0}+\sigma){E}-A]^{-1}B](/morwiki/images/math/d/b/d/dbd7d1f0ea0b36d435e339faa50efd82.png)
![=C[\sigma { E}+(s_{0}{ E}-{ A})]^{-1}B](/morwiki/images/math/6/e/1/6e1b6ff9e81fdab5549d38f82635515a.png)
![=C[{ I}+\sigma(s_0{ E}-{ A})^{-1}E]^{-1}(s_0{ E}-{ A})^{-1}B](/morwiki/images/math/f/0/1/f010b756593ba5d566b421c4886d8de1.png)
![=C[{ I}-\sigma(s_0{ E}- A )^{-1}E+\sigma^2[(s_0{ E}-{ A})^{-1}E]^{2}+\ldots]
(s_0{E}-{ A})^{-1}B](/morwiki/images/math/1/1/1/11171d2f3f9f65584ae574536273d805.png)
![=\sum \limits^\infty_{i=0}\underbrace{C[-(s_0{ E}-{A})^{-1}E]^i(s_0{ E}-{ A})^{-1}B}_{:= m_i(s_0)} \, \sigma^i,](/morwiki/images/math/6/1/f/61fc7e4a1207580a0294f2be5aee3957.png)