1 Description
These first order systems are given in generalized state space form
and originated at CEPEL for simulating large power systems.
They come in different sizes and variants, including both SISO and MIMO systems having regular or singular  matrices. In the latter case the DAEs are of index 1 and using simple row and column permutations,
matrices. In the latter case the DAEs are of index 1 and using simple row and column permutations, 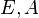 can be brought into the form
can be brought into the form
where 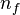 denotes the number of finite eigenvalues in
denotes the number of finite eigenvalues in 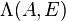 and
and 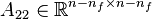 is regular.
A complete overview over these systems can be found in table below. The power systems served as benchmark examples for Dominant Pole based Modal Truncation[1][2][3][4][5] and for a special adaption[6] of Balanced Truncation for the index-1 DAE systems.
is regular.
A complete overview over these systems can be found in table below. The power systems served as benchmark examples for Dominant Pole based Modal Truncation[1][2][3][4][5] and for a special adaption[6] of Balanced Truncation for the index-1 DAE systems.
2 Data
The table below lists the charateristics of all power systems. The files can be downloadet at https://sites.google.com/site/rommes/software.
| Name | 
|
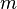
|

|
Type |
|---|---|---|---|---|
| New England | 66 | 1 | 1 | ODE |
| BIPS/97 | 13251 | 1 | 1 | DAE |
| BIPS/1997 | 13250 | 1 | 1 | DAE |
| BIPS/2007 | 21476 | 1 | 1 | DAE |
| BIPS/97,MIMO8 | 13309 | 8 | 8 | DAE |
| BIPS/97,MIMO28 | 13251 | 28 | 28 | DAE |
| BIPS/97,MIMO46 | 13250 | 46 | 46 | DAE |
| Juba5723 | 40337 | 2 | 1 | DAE |
| Bauru5727 | 40366 | 2 | 2 | DAE |
| zeros_nopss | 13296 | 46 | 46 | DAE |
| xingo6u | 20738 | 1 | 6 | DAE |
| nopss | 11685 | 1 | 1 | DAE |
| bips98_606 | 7135 | 4 | 4 | DAE |
| bips98_1142 | 9735 | 4 | 4 | DAE |
| bips98_1450 | 11305 | 4 | 4 | DAE |
| bips07_1693 | 13275 | 4 | 4 | DAE |
| bips07_1998 | 15066 | 4 | 4 | DAE |
| bips07_2476 | 16861 | 4 | 4 | DAE |
| bips07_3078 | 21128 | 4 | 4 | DAE |
| PI Sections 20-80 | ODE |
3 References
<references> [1]
4 Contact
- ↑ 1.0 1.1 N. Martins, L. Lima, and H. Pinto, "Computing dominant poles of power system transfer functions", IEEE Transactions on Power Systems, vol.11, no.1, pp.162-170, 1996
- ↑ 2.0 2.1 J. Rommes and N. Martins, "Efficient computation of transfer function dominant poles using subspace acceleration", IEEE Transactions on Power Systems, vol.21, no.3, pp.1218-1226, 2006
- ↑ 3.0 3.1 J. Rommes and N. Martins, "Efficient computation of multivariable transfer function dominant poles using subspace acceleration", IEEE Transactions on Power Systems, vol.21, no.4, pp.1471-1483, 2006
- ↑ 4.0 4.1 J. Rommes, "Methods for eigenvalue problems with applications in model order reduction", Ph.D. dissertation, Universiteit Utrecht, 2007.
- ↑ 5.0 5.1 P. Kürschner, "Two-sided eigenvalue methods for modal approximation”, Master’s thesis, Chemnitz University of Technology, Department of Mathematics, Germany, 2010.
- ↑ 6.0 6.1 F. Freitas, J. Rommes, and N. Martins, "Gramian-based reduction method applied to large sparse power system descriptor models" IEEE Transactions on Power Systems, vol. 23, no. 3, pp. 1258-1270, 2008.

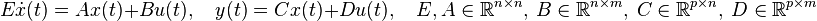
![E=\left[ \begin{array}{cc}I_{n_f}&0\\0&0\end{array}\right],\quad A=\left[ \begin{array}{cc}A_{11}&A_{12}\\A_{21}&A_{22}\end{array}\right],](/morwiki/images/math/a/a/3/aa365f27ce2b7413e4b999bf7569719d.png)