| Background | |
|---|---|
| Benchmark ID |
|
| Category |
power_system |
| System-Class |
LTI-FOS |
| Parameters | |
| nstates |
|
| ninputs |
|
| noutputs |
|
| nparameters |
0 |
| components |
|
| Copyright | |
| License |
NA |
| Creator | |
| Editor | |
| Location | |
|
NA | |
1 Description
These first order systems are given in generalized state space form
where 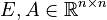 ,
, 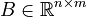 ,
, 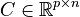 ,
, 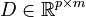 ,
and originated at CEPEL for simulating large power systems.
,
and originated at CEPEL for simulating large power systems.
They come in different sizes and variants, including both SISO and MIMO systems having regular or singular  matrices. In the latter case the DAEs are of index 1 (except for PI Sections 20--80 which are index 2) and using simple row and column permutations,
matrices. In the latter case the DAEs are of index 1 (except for PI Sections 20--80 which are index 2) and using simple row and column permutations, 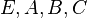 can be brought into the form
can be brought into the form
where 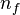 denotes the number of finite eigenvalues in
denotes the number of finite eigenvalues in 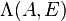 and
and 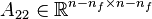 is regular.
A complete overview over these systems can be found in table below. The power systems served as benchmark examples for Dominant Pole based Modal Truncation[1][2][3][4][5][6] and for a special adaption[7] of Balanced Truncation for the index-1 DAE systems.
is regular.
A complete overview over these systems can be found in table below. The power systems served as benchmark examples for Dominant Pole based Modal Truncation[1][2][3][4][5][6] and for a special adaption[7] of Balanced Truncation for the index-1 DAE systems.
2 Data
The table below lists the charateristics of all power systems. The files can be downloaded at https://sites.google.com/site/rommes/software.
| Name | 
|
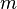
|

|
Type |
|---|---|---|---|---|
| New England | 66 | 1 | 1 | ODE |
| BIPS/97 | 13251 | 1 | 1 | DAE |
| BIPS/1997 | 13250 | 1 | 1 | DAE |
| BIPS/2007 | 21476 | 32 | 32 | DAE |
| BIPS/97,MIMO8 | 13309 | 8 | 8 | DAE |
| BIPS/97,MIMO28 | 13251 | 28 | 28 | DAE |
| BIPS/97,MIMO46 | 13250 | 46 | 46 | DAE |
| Juba5723 | 40337 | 2 | 1 | DAE |
| Bauru5727 | 40366 | 2 | 2 | DAE |
| zeros_nopss | 13296 | 46 | 46 | DAE |
| xingo6u | 20738 | 1 | 6 | DAE |
| nopss | 11685 | 1 | 1 | DAE |
| bips98_606 | 7135 | 4 | 4 | DAE |
| bips98_1142 | 9735 | 4 | 4 | DAE |
| bips98_1450 | 11305 | 4 | 4 | DAE |
| bips07_1693 | 13275 | 4 | 4 | DAE |
| bips07_1998 | 15066 | 4 | 4 | DAE |
| bips07_2476 | 16861 | 4 | 4 | DAE |
| bips07_3078 | 21128 | 4 | 4 | DAE |
| PI Sections: | ||||
| S10 | 682 | 1 | 1 | DAE |
| S20 | 1182 | 1 | 1 | DAE |
| S40 | 2182 | 1 | 1 | DAE |
| S80 | 4182 | 1 | 1 | DAE |
| M10 | 682 | 3 | 3 | DAE |
| M20 | 1182 | 3 | 3 | DAE |
| M40 | 2182 | 3 | 3 | DAE |
| M80 | 4182 | 3 | 3 | DAE |
3 Background
Electrical power systems experience several steady-state and dynamic phenomena that may hinder its reliable, stable operation if not properly designed and operated. Among the dynamic phenomena, power system angle stability is of major concern, its studies requiring both numerical integration of a stiff set of large, nonlinear differential-algebraic (DAE) equations (for transient stability simulations) and the eigensolution as well as the use of other numerical linear algebra (NLA) algorithms applied to the linearized DAE equations of the same large stability models. Power systems with multiple electrical power plants, consumer loads, and industrial loads experience complex electromechanical oscillations, much as spring-mass mechanical systems experience mechanical oscillations. These oscillations, when the electric power system is under stressed conditions, may become poorly damped or unstable. The analysis of these low-frequency oscillations, as well as their controller-induced damping control, is enhanced by the results from NLA algorithms. The study of all these issues constitutes the field known as small signal stability.
There is a pressing need for better utilization of the transmission network and its cost-effective expansions to reliably carry electric power from the generating plants, driven by several primary energy sources, to the loads. This imposes stricter requirements on network design and power system control equipment, as well as on the adopted control laws, which, coupled with the continental dimensions of modern interconnected power systems, must be studied with the help of simulators employing advanced NLA algorithms. This wiki page contains system models developed when dealing with these NLA issues, with emphasis on the analysis and control of small signal stability.
Modal analysis has been used for Model Order Reduction (MOR) of lightly damped systems like flexible mechanical structures and RLC networks from either power systems or microprocessor interconnectors. The advent of subspace accelerated dominant pole algorithms in [1][2][3], made modal reduction effective for better damped systems, such as interconnected power systems, which have eigenvalue clusters in the 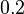 to
to 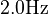 range and damping ratios between
range and damping ratios between 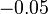 and
and 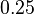 . Important characteristics of model reduction methods include preserving the dominant dynamics and stability in the Reduced Order Models (ROMs).
. Important characteristics of model reduction methods include preserving the dominant dynamics and stability in the Reduced Order Models (ROMs).
Model reduction is important to the linear control system analysis and design of power system dynamic models. Reduced-order power system transfer function models are effective in lowering the computational costs of controller design. Once the dominant transfer function poles have been found, the calculation of their associated residues can be obtained by the scalar product of the left and right eigenvectors by the input and output vectors of the transfer function. From the knowledge of the dominant pole-residue set, one can build a transfer function ROM whose accuracy varies with the number of retained poles. See, e.g., the SADPA, SAMDP papers [2][3].
Modal analysis is also used in the harmonic distortion analysis of power system networks, mainly in subtransmission and distribution voltage levels. In this application, modal analysis allows for determining the main network parameters that impact distortion levels and suggests changes to their effective values among other alternatives. The linear RLC network is modeled unloaded, the conventional electrical generators can be entirely neglected and the nonlinear loads of various nature are modeled as current injections into the network buses -3rd, 5th, 7th, 11th, 13th harmonics of the nominal system frequency (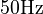 or
or 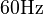 ). An even more important application for the modal analysis of these large descriptor system RLC network models is the production of ROM for multiport electrical networks, generally in the form of a state-space system whose dimension is considerably smaller than that of the original system. When these ROMs take the form of RLC networks, they are referred to as RLC reduced equivalents. These ROMs, or equivalents, are used in real-time and off-line simulators for the study of power system high-frequency transient phenomena. They are produced in varying degrees of complexity by using advanced NLA algorithms, which is an area of intense research work.
). An even more important application for the modal analysis of these large descriptor system RLC network models is the production of ROM for multiport electrical networks, generally in the form of a state-space system whose dimension is considerably smaller than that of the original system. When these ROMs take the form of RLC networks, they are referred to as RLC reduced equivalents. These ROMs, or equivalents, are used in real-time and off-line simulators for the study of power system high-frequency transient phenomena. They are produced in varying degrees of complexity by using advanced NLA algorithms, which is an area of intense research work.
4 Test systems for small-signal stability analysis of large electric power system networks
All test power systems in https://sites.google.com/site/rommes/software, except the PI sections example, are used for power system small-signal stability studies, and several of them are briefly described in [1]. Such studies include stability analysis, controller design, computation of MOR, etc. The dynamic phenomena of interest require the detailed modeling of the electrical energy generators (mainly the large sized ones) and other important devices such as flexible AC transmission systems (FACTS). The 3-phase alternating current (AC) network consists of nodes (electrical buses), which may be the representation of an entire electrical energy transmission (or distribution) substation, and branches (transmission lines, transformers, series capacitors) and need to have only a static model in this application except for the occasional high-power electronic HVDC (High voltage direct current) transmission links and FACTS devices.
The input  depends on the study of interest, but the excitation system voltage reference is a frequent input variable in small-signal stability studies. Another reference is the active power setpoint of a rotor-speed regulator. The input signal used in all the above-mentioned files is of Vref type. The output could be an entry of the generalized state
depends on the study of interest, but the excitation system voltage reference is a frequent input variable in small-signal stability studies. Another reference is the active power setpoint of a rotor-speed regulator. The input signal used in all the above-mentioned files is of Vref type. The output could be an entry of the generalized state 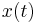 (state or algebraic variable) or a linear combination of these variables. The generalized states
(state or algebraic variable) or a linear combination of these variables. The generalized states 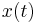 are associated with equations of generators, controllers, and network. The interconnected network has only algebraic variables, except when FACTS devices are connected.
The test systems are represented by generalized state-space models, see above, where the feed through matrix
are associated with equations of generators, controllers, and network. The interconnected network has only algebraic variables, except when FACTS devices are connected.
The test systems are represented by generalized state-space models, see above, where the feed through matrix 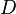 is generally zero.
is generally zero.
5 Test systems for electromagnetic transients and harmonic distortion studies
Depending on the harmonic study at hand, a voltage or current source can be assigned as an input. In [1] the current injection  at a node (also, electrical bus, in power system terminology) is the input, while the nodal voltage, at the same node, is the output (variable
at a node (also, electrical bus, in power system terminology) is the input, while the nodal voltage, at the same node, is the output (variable  ).
).
All transmission lines in the network are modeled by RLC ladder networks, of cascaded RLC PI-circuits, having fixed parameters [8]. The transformers are modeled by series RL circuits. Loads and shunt elements are represented by series-connected RL (or RC) branch, or just an L (or C). As a consequence, the states 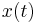 of the dynamic system are either the current through an inductor or the voltage across a capacitor. So matrices
of the dynamic system are either the current through an inductor or the voltage across a capacitor. So matrices 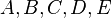 describe how each circuit element equation, node and voltage are connected, according to the Kirchhoff’s law.
describe how each circuit element equation, node and voltage are connected, according to the Kirchhoff’s law.
On https://sites.google.com/site/rommes/software the systems labeled by PI Sections 20--80 are of index-2 (SISO_PI_n.zip and MIMO_PI_n.zip). The data of these test systems can be converted into index-0 systems by applying a procedure for symbolic math elimination of algebraic variables and redundant state variables. This procedure is detailed in the Appendix C of [9].
6 References
- ↑ 1.0 1.1 1.2 1.3 N. Martins, L. Lima, and H. Pinto, "Computing dominant poles of power system transfer functions", IEEE Transactions on Power Systems, 11: 162--170, 1996.
- ↑ 2.0 2.1 2.2 J. Rommes and N. Martins, "Efficient computation of transfer function dominant poles using subspace acceleration", IEEE Transactions on Power Systems, 21(3): 1218--1226, 2006.
- ↑ 3.0 3.1 3.2 J. Rommes and N. Martins, "Efficient computation of multivariable transfer function dominant poles using subspace acceleration", IEEE Transactions on Power Systems, 21(4): 1471--1483, 2006.
- ↑ J. Rommes, "Methods for eigenvalue problems with applications in model order reduction", Ph.D. dissertation, Universiteit Utrecht, 2007.
- ↑ J. Rommes and N. Martins, "Computing transfer function dominant poles of large second-order dynamical systems" SIAM Journal on Scientific Computing, 30(4): 2137--2157, 2008.
- ↑ P. Kürschner, "Two-sided eigenvalue methods for modal approximation”, Master’s thesis, Chemnitz University of Technology, Department of Mathematics, Germany, 2010.
- ↑ F. Freitas, J. Rommes, and N. Martins, "Gramian-based reduction method applied to large sparse power system descriptor models" IEEE Transactions on Power Systems, 23(3): 1258--1270, 2008.
- ↑ N. Watson and J. Arrillaga, "Power Systems Electromagnetic Transients Simulation”, IET, London, UK, 2003.
- ↑ F. D. Freitas, N. Martins, S. L. Varricchio, J. Rommes and F. C. Veliz, "Reduced-Order Transfer Matrices from RLC Network Descriptor Models of Electric Power Grids” IEEE Transactions on Power Systems, 26(4): 1905--1916, 2011.
7 Contact
Joost Rommes
Patrick Kürschner
Nelson Martins
Francisco D. Freitas

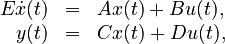
![E=\left[ \begin{array}{cc}I_{n_f}&0\\0&0\end{array}\right],\quad A=\left[ \begin{array}{cc}A_{11}&A_{12}\\A_{21}&A_{22}\end{array}\right],\quad B=\left[ \begin{array}{cc}B_{1}\\B_2\end{array}\right],\quad C=\left[ \begin{array}{cc}C_{1}&C_2\end{array}\right],](/morwiki/images/math/e/1/9/e19ed16a38d6d2d2563fe746dda78fbe.png)