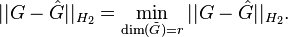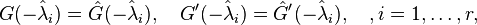Iterative Rational Krylov Algorithm

Description

The iterative rational Krylov algorithm (IRKA) is an interpolation-based model reduction method for single-input-single-output linear time invariant systems

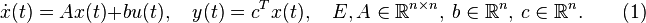$\dot{x}(t)=A x(t)+b u(t), \quad y(t)=c^Tx(t),\quad E,A\in\mathbb{R}^{n\times n},~b\in\mathbb{R}^{n},~c\in\mathbb{R}^{n}.\qquad (1)$ (1)

For a given system 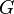$G$ and a prescribed reduced system order $r$, the goal of the algorithm is to find a local minimizer 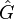$\hat{G}$ for the 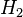$H_2$ model reduction problem

$||G-\hat{G} ||_{H_2} = \min_{\text{dim}(\tilde{G})=r} ||G-\hat{G}||_{H_2}.$

Initially investigated in , first order necessary conditions for a local minimizer 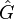$\hat{G}$ imply that its rational transfer function 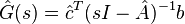$\hat{G}(s)=\hat{c}^T (sI-\hat{A})^{-1}b$ is a Hermite interpolant of the original transfer function at its reflected system poles, i.e.,

$G(-\hat{\lambda}_i) = \hat{G}(-\hat{\lambda}_i), \quad G'(-\hat{\lambda}_i) = \hat{G}'(-\hat{\lambda}_i), \quad, i =1,\dots,r,$

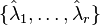where $\{\hat{\lambda}_1,\dots,\hat{\lambda}_r\}$ are assumed to be the simple poles of 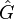$\hat{G}$. Based on the idea of rational interpolation by rational Krylov subspaces, in the authors have picked up the optimality conditions and proposed to iteratively correct projection subspaces until interpolation is ensured. In pseudocode, the classical algorithm (IRKA) from looks like

1. Make an initial selection of $\sigma_i$ for $i=1,\dots,r$ that is closed under conjugation and fix a convergence tolerance $tol$.
2. Choose $V_r$ and $W_r$ so that $\text{Ran}(V_r) =\{(\sigma_1 I -A)^{-1}b,\dots,(\sigma_rI-A)^{-1}b \}$, $\text{Ran}(W_r) =\{(\sigma_1 I -A^T)^{-1}c,\dots,   (\sigma_rI-A^T)^{-1}c \}$ and $W_r^TV_r=I$.
3. while (relative change in $\{\sigma_i\} > tol$)
 (a) $\hat{A} = W_r^TAV_r$
 (b) Assign $\sigma_i \leftarrow -\lambda_i(\hat{A}),$ for $i=1,\dots,r$
 (c) Update $V_r$ and $W_r$ so that $\text{Ran}(V_r) =\{(\sigma_1 I -A)^{-1}b,\dots,(\sigma_rI-A)^{-1}b \}$, $\text{Ran}(W_r) =\{(\sigma_1 I -A^T)^{-1}c,\dots,   (\sigma_rI-A^T)^{-1}c \}$ and $W_r^TV_r=I$.
4. $\hat{A} = W_r^TAV_r, \hat{b}= W_r^Tb, \hat{c}^T = c^TV_r.$

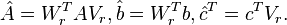
Although a rigorous convergence proof so far has only be given for symmetric state space systems , numerous experiments have shown that the algorithm often converges rapidly.

References

<references>

</ references>