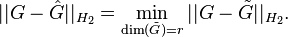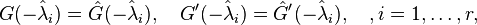Iterative Rational Krylov Algorithm

Description

IRKA (iterative rational Krylov algorithm) is an interpolation-based model reduction method for SISO linear time invariant systems.

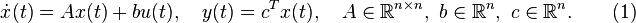\dot{x}(t)=A x(t)+b u(t), \quad y(t)=c^Tx(t),\quad A\in\mathbb{R}^{n\times n},~b\in\mathbb{R}^{n},~c\in\mathbb{R}^{n}.\qquad (1)

(1)

For a given system 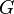$G$ and a prescribed reduced system order $r$ , the goal of the algorithm is to find a local minimizer 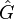$\hat{G}$ for the 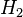$H_2$ model reduction problem

||G-\hat{G} ||_{H_2} = \min_{\text{dim}(\tilde{G})=r} ||G-\tilde{G}||_{H_2}.

Initially investigated in ^[1], first order necessary conditions for a local minimizer 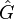$\hat{G}$ imply that its rational transfer function 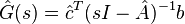$\hat{G}(s)=\hat{c}^T (sI-\hat{A})^{-1}b$ is a Hermite interpolant of the original transfer function at its reflected system poles, i.e.,

G(-\hat{\lambda}_i) = \hat{G}(-\hat{\lambda}_i), \quad G'(-\hat{\lambda}_i) = \hat{G}'(-\hat{\lambda}_i), \quad, i =1,\dots,r,

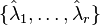where $\{\hat{\lambda}_1,\dots,\hat{\lambda}_r\}$ are assumed to be the simple poles of 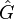$\hat{G}$ . Based on the idea of rational interpolation by rational Krylov subspaces, in ^[2] the authors have picked up the optimality conditions and proposed to iteratively correct projection subspaces until interpolation at the reflected reduced system poles is ensured. In pseudocode, the classical IRKA algorithm from ^[2] looks like

1. Make an initial selection of  $\sigma_i$  for  $i=1,\dots,r$  that is closed under conjugation and fix a convergence tolerance  $tol$ .
2. Choose  $V_r$  and  $W_r$  so that  $\text{Ran}(V_r) =\{(\sigma_1 I -A)^{-1}b,\dots,(\sigma_rI-A)^{-1}b \}$ ,  $\text{Ran}(W_r) =\{(\sigma_1 I -A^T)^{-1}c,\dots, (\sigma_rI-A^T)^{-1}c \}$  and  $W_r^TV_r=I$ .
3. while (relative change in  $\{\sigma_i\} > tol$ )
 (a)  $\hat{A} = W_r^TAV_r$ 
 (b) Assign  $\sigma_i \leftarrow -\lambda_i(\hat{A}),$  for  $i=1,\dots,r$ 
 (c) Update  $V_r$  and  $W_r$  so that  $\text{Ran}(V_r) =\{(\sigma_1 I -A)^{-1}b,\dots,(\sigma_rI-A)^{-1}b \}$ ,  $\text{Ran}(W_r) =\{(\sigma_1 I -A^T)^{-1}c,\dots, (\sigma_rI-A^T)^{-1}c \}$  and  $W_r^TV_r=I$ .
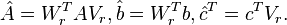
4.  $\hat{A} = W_r^TAV_r, \hat{b}= W_r^Tb, \hat{c}^T = c^TV_r.$

Although a rigorous convergence proof so far has only be given for symmetric state space systems ^[3], numerous experiments have shown that the algorithm often converges rapidly. Moreover, the algorithm has been extended to, e.g., multiple-input-multiple output, discrete time and differential algebraic systems.

A minimal example

For the lecture Model MOR of Mechanical System from the Institute of Engineering and Computational Mechanics University of Stuttgart a very simple example of the IRKA Algorithm were written.

The implementation with two basic exampless can be found here

Media:IRKA_Example.zip

References

↑ L. Meier, D.G. Luenberger, "Approximation of linear constant systems", IEEE Transactions on Automatic Control, vol.12, no.5, pp.585-588, 1967.
↑ ^2.0 ^2.1 S. Gugercin, A.C. Antoulas, C. Beattie "H2 Model Reduction for Large-Scale Linear Dynamical Systems", SIAM. J. Matrix Anal. & Appl., vol.30, no.2, pp.609-638, 2008.
↑ G. Flagg, C. Beattie, S. Gugercin "Convergence of the Iterative Rational Krylov Algorithm", Systems & Control Letters, vol.61, no.6, pp.688-691, 2012.

[MeiL67-1] L. Meier, D.G. Luenberger, "Approximation of linear constant systems", IEEE Transactions on Automatic Control, vol.12, no.5, pp.585-588, 1967.

[GugAB08-2] 2.0 ^2.1 S. Gugercin, A.C. Antoulas, C. Beattie "H2 Model Reduction for Large-Scale Linear Dynamical Systems", SIAM. J. Matrix Anal. & Appl., vol.30, no.2, pp.609-638, 2008.

[FlaBG12-3] G. Flagg, C. Beattie, S. Gugercin "Convergence of the Iterative Rational Krylov Algorithm", Systems & Control Letters, vol.61, no.6, pp.688-691, 2012.

[1]

[2]

[3]