Description of physical model
Preparative liquid chromatography as a crucial separation and purification tool has been widely employed in food, fine chemical and pharmaceutical industries. Chromatographic separation at industry scale can be operated either discontinuously or in a continuous mode. The continuous case will be addressed in the benchmark SMB, and here we focus on the discontinuous mode -- batch chromatography.
The dynamics of the batch chromatographics column can be described precisely by an axially dispersed plug-flow model with a limited mass-transfer rate characterized by a linear driving force (LDF) approximation. In this model the differential mass balance of component  (
(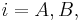 )
in the liquid phase can be written as:
)
in the liquid phase can be written as:
![\frac{\partial c_i}{\partial t}+\frac{1-\epsilon}{\epsilon}\frac{\partial q_i}{\partial t}+u\frac{\partial c_i}{\partial z}-D_i\frac{\partial^2 c_i}{\partial z^2}=0, \qquad z\in(0,\;L), \qquad [1]](/morwiki/images/math/2/9/c/29c6e31475552611f8af57edcbf91591.png)
where 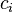 and
and 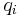 are the concentrations of solute $i$ in the liquid and solid phases, respectively, $u$ the interstitial liquid velocity,
are the concentrations of solute $i$ in the liquid and solid phases, respectively, $u$ the interstitial liquid velocity, 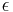 the column porosity,
the column porosity, 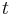 the time coordinate,
the time coordinate, 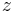 the axial coordinate along the column,
the axial coordinate along the column, 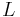 the column length,
the column length, 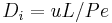 the axial dispersion coefficient and
the axial dispersion coefficient and 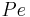 the P\'{e}clet number. The adsorption rate is modeled by the LDF approximation:
the P\'{e}clet number. The adsorption rate is modeled by the LDF approximation:
![\frac{\partial q_i}{\partial t} = K_{m,i}\,(q^{Eq}_i-q_i), \qquad z\in[0,\;L], \qquad [2]](/morwiki/images/math/2/b/c/2bccfd7a335642719a5fc23201c6bdd7.png)
where 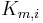 is the mass-transfer coefficient of component
is the mass-transfer coefficient of component  and
and 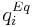 is the adsorption equilibrium concentration calculated by the isotherm equation for component
is the adsorption equilibrium concentration calculated by the isotherm equation for component  . Here the bi-Langmuir isotherm model is used to describe the adsorption equilibrium:
. Here the bi-Langmuir isotherm model is used to describe the adsorption equilibrium:
![q^{Eq}_i=\frac{H_{i,1}\,c_i}{1+\sum_{j=A,B}K_{j,1}\,c_j}+\frac{H_{i,2}\,c_i}{1+\sum_{j=A,B}K_{j,2}\,c_j},\; i=A,B, \qquad [3]](/morwiki/images/math/2/2/b/22bb74b0de50b419926f82a300a1dd1b.png) where
where 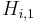 and
and 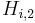 are the Henry constants, and
are the Henry constants, and 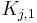 and
and 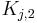 the thermodynamic coefficients.
the thermodynamic coefficients.
The boundary conditions for Eq. [] are specified by the Danckwerts relations:
![D_i\left.\frac{\partial c_i}{\partial z}\right|_{z=0} = u\,(\left.c_i\right|_{z=0}-c^{in}_i), \quad\quad \left.\frac{\partial c_i}{\partial z}\right|_{z=L}=0, \qquad [4]](/morwiki/images/math/1/f/7/1f7d9e0d253e134573e0eb70f37d8315.png)
where 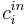 is the concentration of component
is the concentration of component  at the inlet of the column. A rectangular injection is assumed for the system and thus
at the inlet of the column. A rectangular injection is assumed for the system and thus
Failed to parse (syntax error): c^{in}_i=\left { \begin{array}{cc} c^F_i, &\text{if } t \le t_{inj};\\ 0, &\text{if } t > t_{inj}. \right . \end{array}
where 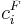 is the feed concentration for component
is the feed concentration for component  and
and 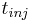 is the injection period. In addition, the column is assumed unloaded initially:
is the injection period. In addition, the column is assumed unloaded initially:
![c_i(t=0,z)=q_i(t=0,z)=0,\quad z\in[0,\;L],\;i=A,B. \qquad [5]](/morwiki/images/math/9/6/2/962c668ca053158ec68ef998d0fcdd90.png)
