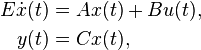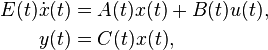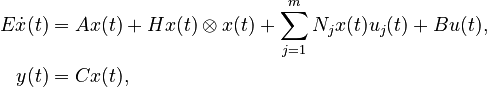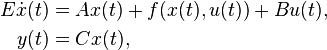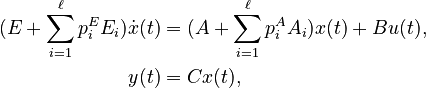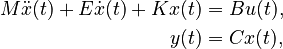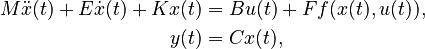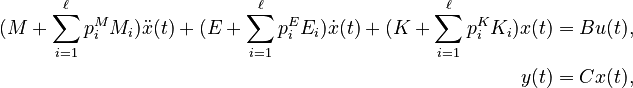(→Nonlinear Second-Order System: add F matrix to nonlinear term (see Electrostatic Beam)) |
m (standardize parameter indices; clean up how u_j is defined; revert Q back to H for QBS) |
||
| Line 1: | Line 1: | ||
{{preliminary}} <!-- Do not remove --> |
{{preliminary}} <!-- Do not remove --> |
||
| − | [[Category: |
+ | [[Category:Benchmarks]] |
| − | ==Benchmark Model |
+ | ==Benchmark Model Templates== |
| + | This page specifies templates for the types of models used as benchmark systems. In particular, the naming schemes established here are used in the corresponding data sets for all benchmarks. For example, <math>A</math> always serves as the name of the component matrix applied to the state <math>x(t)</math> in a linear time-invariant system. |
||
| − | This page outlines the types of models that are used as benchmark systems. |
||
| − | For |
+ | For all models we assume an input <math>u : \mathbb{R} \to \mathbb{R}^m</math>, with components <math>u_j, j = 1, \ldots, m</math>, |
| − | a state <math>x : \mathbb{R} \to \mathbb{R}^n</math> |
+ | a state <math>x : \mathbb{R} \to \mathbb{R}^n</math>, |
| ⚫ | |||
===Linear Time-Invariant System=== |
===Linear Time-Invariant System=== |
||
| Line 17: | Line 18: | ||
</math> |
</math> |
||
| − | with |
+ | with |
<math>E \in \mathbb{R}^{n \times n}</math>, |
<math>E \in \mathbb{R}^{n \times n}</math>, |
||
| Line 34: | Line 35: | ||
</math> |
</math> |
||
| − | with |
+ | with |
<math>E : \mathbb{R} \to \mathbb{R}^{n \times n}</math>, |
<math>E : \mathbb{R} \to \mathbb{R}^{n \times n}</math>, |
||
| Line 46: | Line 47: | ||
:<math> |
:<math> |
||
\begin{align} |
\begin{align} |
||
| − | E\dot{x}(t) &= A x(t) + |
+ | E\dot{x}(t) &= A x(t) + H x(t) \otimes x(t) + \sum_{j=1}^m N_j x(t) u_j(t) + B u(t), \\ |
y(t) &= Cx(t), |
y(t) &= Cx(t), |
||
\end{align} |
\end{align} |
||
</math> |
</math> |
||
| − | with |
+ | with |
<math>E \in \mathbb{R}^{n \times n}</math>, |
<math>E \in \mathbb{R}^{n \times n}</math>, |
||
<math>A \in \mathbb{R}^{n \times n}</math>, |
<math>A \in \mathbb{R}^{n \times n}</math>, |
||
| − | <math> |
+ | <math>H \in \mathbb{R}^{n \times n^2}</math>, |
| − | <math> |
+ | <math>N_j \in \mathbb{R}^{n \times n}</math>, |
| ⚫ | |||
<math>B \in \mathbb{R}^{n \times m}</math>, |
<math>B \in \mathbb{R}^{n \times m}</math>, |
||
<math>C \in \mathbb{R}^{q \times n}</math>. |
<math>C \in \mathbb{R}^{q \times n}</math>. |
||
| Line 70: | Line 70: | ||
</math> |
</math> |
||
| − | with |
+ | with |
<math>E \in \mathbb{R}^{n \times n}</math>, |
<math>E \in \mathbb{R}^{n \times n}</math>, |
||
| Line 83: | Line 83: | ||
:<math> |
:<math> |
||
\begin{align} |
\begin{align} |
||
| − | ( |
+ | (E + \sum_{i=1}^{\ell} p^E_i E_i)\dot{x}(t) &= (A + \sum_{i=1}^{\ell} p^A_i A_i) x(t) + Bu(t),\\ |
y(t) &= Cx(t), |
y(t) &= Cx(t), |
||
\end{align} |
\end{align} |
||
</math> |
</math> |
||
| − | with |
+ | with |
| − | <math> |
+ | <math>E \in \mathbb{R}^{n \times n}</math>, |
| − | <math> |
+ | <math>E_i \in \mathbb{R}^{n \times n}</math>, |
| − | <math> |
+ | <math>A \in \mathbb{R}^{n \times n}</math>, |
<math>A_i \in \mathbb{R}^{n \times n}</math>, |
<math>A_i \in \mathbb{R}^{n \times n}</math>, |
||
<math>B \in \mathbb{R}^{n \times m}</math>, |
<math>B \in \mathbb{R}^{n \times m}</math>, |
||
| Line 106: | Line 106: | ||
</math> |
</math> |
||
| − | with |
+ | with |
<math>M \in \mathbb{R}^{n \times n}</math>, |
<math>M \in \mathbb{R}^{n \times n}</math>, |
||
| Line 123: | Line 123: | ||
</math> |
</math> |
||
| − | with |
+ | with |
<math>M \in \mathbb{R}^{n \times n}</math>, |
<math>M \in \mathbb{R}^{n \times n}</math>, |
||
| Line 137: | Line 137: | ||
:<math> |
:<math> |
||
\begin{align} |
\begin{align} |
||
| − | ( |
+ | (M + \sum_{i=1}^{\ell} p^M_i M_i)\ddot{x}(t) + (E + \sum_{i=1}^{\ell} p^E_i E_i)\dot{x}(t) + (K + \sum_{i=1}^{\ell} p^K_i K_i)x(t) &= B u(t), \\ |
y(t) &= C x(t), |
y(t) &= C x(t), |
||
\end{align} |
\end{align} |
||
</math> |
</math> |
||
| − | with |
+ | with |
| − | <math> |
+ | <math>M \in \mathbb{R}^{n \times n}</math>, |
<math>M_i \in \mathbb{R}^{n \times n}</math>, |
<math>M_i \in \mathbb{R}^{n \times n}</math>, |
||
| − | <math> |
+ | <math>E \in \mathbb{R}^{n \times n}</math>, |
| − | <math> |
+ | <math>E_i \in \mathbb{R}^{n \times n}</math>, |
| − | <math> |
+ | <math>K \in \mathbb{R}^{n \times n}</math>, |
| − | <math> |
+ | <math>K_i \in \mathbb{R}^{n \times n}</math>, |
<math>B \in \mathbb{R}^{n \times m}</math>, |
<math>B \in \mathbb{R}^{n \times m}</math>, |
||
<math>C \in \mathbb{R}^{q \times n}</math>. |
<math>C \in \mathbb{R}^{q \times n}</math>. |
||
Revision as of 14:33, 25 August 2022
 Note: This page has not been verified by our editors.
Note: This page has not been verified by our editors.
Benchmark Model Templates
This page specifies templates for the types of models used as benchmark systems. In particular, the naming schemes established here are used in the corresponding data sets for all benchmarks. For example,  always serves as the name of the component matrix applied to the state
always serves as the name of the component matrix applied to the state 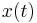 in a linear time-invariant system.
For all models we assume an input
in a linear time-invariant system.
For all models we assume an input 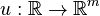 , with components
, with components 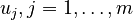 ,
a state
,
a state 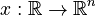 ,
and an output
,
and an output 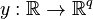 .
.
Linear Time-Invariant System
with
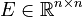 ,
,
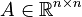 ,
,
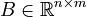 ,
,
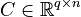 .
.
Linear Time-Varying System
with
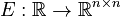 ,
,
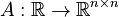 ,
,
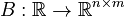 ,
,
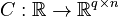 .
.
Quadratic-Bilinear System
with
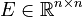 ,
,
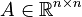 ,
,
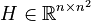 ,
,
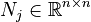 ,
,
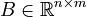 ,
,
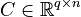 .
.
Nonlinear Time-Invariant System
with
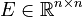 ,
,
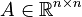 ,
,
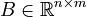 ,
,
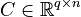 ,
,
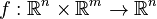 .
.
Affine Parametric Linear Time-Invariant System
with
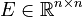 ,
,
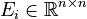 ,
,
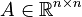 ,
,
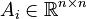 ,
,
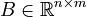 ,
,
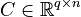 .
.
Second-Order System
with
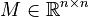 ,
,
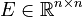 ,
,
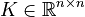 ,
,
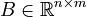 ,
,
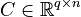 .
.
Nonlinear Second-Order System
with
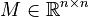 ,
,
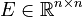 ,
,
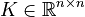 ,
,
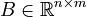 ,
,
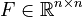 ,
,
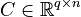 ,
,
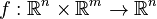 .
.
Affine Parametric Second-Order System
with
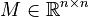 ,
,
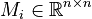 ,
,
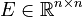 ,
,
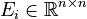 ,
,
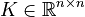 ,
,
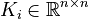 ,
,
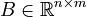 ,
,
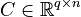 .
.