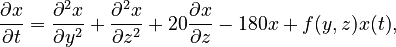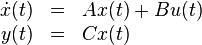(Add equation and fix link.) |
(update description.) |
||
| Line 17: | Line 17: | ||
</math> |
</math> |
||
| − | with Dirichlet boundary conditions. |
+ | with Dirichlet boundary conditions and discretized with centered difference approximation. |
| − | The output vector equals the input vector <math>C = B^T</math> |
+ | The input vector <math>B</math> is composed of random elements and the output vector equals the input vector <math>C = B^T</math>. |
More details can be found in <ref name="raschman80"/>, <ref name="saad88"/>, <ref name="grimme97"/> and <ref name="chahlaoui02"/>, <ref name="chahlaoui05"/>. |
More details can be found in <ref name="raschman80"/>, <ref name="saad88"/>, <ref name="grimme97"/> and <ref name="chahlaoui02"/>, <ref name="chahlaoui05"/>. |
||
Revision as of 11:18, 2 December 2021
 Note: This page has not been verified by our editors.
Note: This page has not been verified by our editors.
This is a stub. Please expand.
Description
This benchmark models a chemical reaction by a convection-reaction partial differential equation on the unit square, given by:
with Dirichlet boundary conditions and discretized with centered difference approximation.
The input vector  is composed of random elements and the output vector equals the input vector
is composed of random elements and the output vector equals the input vector 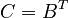 .
.
More details can be found in [1], [2], [3] and [4], [5].
Origin
This benchmark is part of the SLICOT Benchmark Examples for Model Reduction[5].
Data
The system matrices  ,
,  ,
,  are available from the SLICOT benchmarks page: pde.zip and are stored as MATLAB .mat file.
are available from the SLICOT benchmarks page: pde.zip and are stored as MATLAB .mat file.
Dimensions
System structure:
System dimensions:
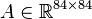 ,
,
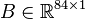 ,
,
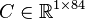 .
.
Citation
To cite this benchmark, use the following references:
- For the benchmark itself and its data:
- Niconet e.V., SLICOT - Subroutine Library in Systems and Control Theory, http://www.slicot.org
@MANUAL{slicot_pde,
title = {{SLICOT} - Subroutine Library in Systems and Control Theory},
organization = {Niconet e.V.},
address = {\url{http://www.slicot.org}},
key = {SLICOT}
}
- For the background on the benchmark:
@ARTICLE{Saa88,
author = {Y. Saad},
title = {Projection and deflation method for partial pole assignment in linear state feedback},
journal = {IEEE Transactions on Automatic Control},
volume = {33},
number = {3},
pages = {290--297},
year = {1988},
doi = {10.1109/9.406}
}
References
- ↑ P. Raschman, M. Kuhicek, M. Maros. Waves in distributed chemical systems: Experiments and computations. In: New Approaches to Nonlinear Problems in Dynamics - Proceedings of the Asilomar Conference Ground: 271--288, SIAM, 1980.
- ↑ Y. Saad. Projection and deflation method for partial pole assignment in linear state feedback, IEEE Transactions on Automatic Control, 33(3): 290--297, 1988.
- ↑ E.J. Grimme. Krylov Projection Methods for Model Reduction. PhD Thesis, University of Illinois at Urbana-Champaign, 1998.
- ↑ Y. Chahlaoui, P. Van Dooren, A collection of Benchmark examples for model reduction of linear time invariant dynamical systems, Working Note 2002-2: 2002.
- ↑ 5.0 5.1 Y. Chahlaoui, P. Van Dooren, Benchmark Examples for Model Reduction of Linear Time-Invariant Dynamical Systems, Dimension Reduction of Large-Scale Systems, Lecture Notes in Computational Science and Engineering, vol 45: 379--392, 2005.