m (references with cite, reference link) |
m (equation indent) |
||
| Line 16: | Line 16: | ||
The exact, infinite-dimensional formulation, indicated by the superscript e, is given by |
The exact, infinite-dimensional formulation, indicated by the superscript e, is given by |
||
| ⚫ | |||
| − | |||
| ⚫ | |||
\begin{cases} |
\begin{cases} |
||
\text{For } \mu \in \mathcal{D} \subset \mathbb{R}^P, \text{ evaluate } \\ |
\text{For } \mu \in \mathcal{D} \subset \mathbb{R}^P, \text{ evaluate } \\ |
||
| Line 28: | Line 27: | ||
Through spatial discretization, e.g. finite element method, we consider the discretized system |
Through spatial discretization, e.g. finite element method, we consider the discretized system |
||
| − | <math> |
+ | :<math> |
\begin{cases} |
\begin{cases} |
||
\text{For } \mu \in \mathcal{D} \subset \mathbb{R}^P, \text{ evaluate } \\ |
\text{For } \mu \in \mathcal{D} \subset \mathbb{R}^P, \text{ evaluate } \\ |
||
| Line 45: | Line 44: | ||
The essential assumption which allows the offline-online decomposition is that there exists an affine parameter dependence |
The essential assumption which allows the offline-online decomposition is that there exists an affine parameter dependence |
||
| − | <math> |
+ | :<math> |
a(w,v;\mu) = \sum_{q=1}^{Q^a} \Theta_a^q(\mu) a^q(w,v) |
a(w,v;\mu) = \sum_{q=1}^{Q^a} \Theta_a^q(\mu) a^q(w,v) |
||
</math> |
</math> |
||
| − | <math> |
+ | :<math> |
f(v;\mu) = \sum_{q=1}^{Q^f} \Theta_f^{q}(\mu) f^q(v). |
f(v;\mu) = \sum_{q=1}^{Q^f} \Theta_f^{q}(\mu) f^q(v). |
||
</math> |
</math> |
||
| Line 55: | Line 54: | ||
The Lagrange Reduced Basis space is established by iteratively choosing Lagrange parameter samples |
The Lagrange Reduced Basis space is established by iteratively choosing Lagrange parameter samples |
||
| − | <math> |
+ | :<math> |
S_N = \{\mu^1,...,\mu^N\} |
S_N = \{\mu^1,...,\mu^N\} |
||
</math> |
</math> |
||
| Line 61: | Line 60: | ||
and considering the associated Lagrange RB spaces |
and considering the associated Lagrange RB spaces |
||
| − | <math> |
+ | :<math> |
V_N = \text{span}\{u(\mu^n), 1 \leq n \leq N \} |
V_N = \text{span}\{u(\mu^n), 1 \leq n \leq N \} |
||
</math> |
</math> |
||
| Line 69: | Line 68: | ||
We then consider the galerkin projection onto the RB-space <math> V_N </math> |
We then consider the galerkin projection onto the RB-space <math> V_N </math> |
||
| − | <math> |
+ | :<math> |
\begin{cases} |
\begin{cases} |
||
\text{For } \mu \in \mathcal{D} \subset \mathbb{R}^P, \text{ evaluate } \\ |
\text{For } \mu \in \mathcal{D} \subset \mathbb{R}^P, \text{ evaluate } \\ |
||
| Line 103: | Line 102: | ||
The exact, infinite-dimensional formulation, indicated by the superscript e, is given by |
The exact, infinite-dimensional formulation, indicated by the superscript e, is given by |
||
| − | <math> |
+ | :<math> |
\begin{cases} |
\begin{cases} |
||
\text{For } \mu \in \mathcal{D} \subset \mathbb{R}^P, t^k \in [0,T] \text{ evaluate } \\ |
\text{For } \mu \in \mathcal{D} \subset \mathbb{R}^P, t^k \in [0,T] \text{ evaluate } \\ |
||
| Line 117: | Line 116: | ||
Assume a reference discretization form is given as follows, |
Assume a reference discretization form is given as follows, |
||
| − | <math> |
+ | :<math> |
\begin{cases} |
\begin{cases} |
||
\text{For } \mu \in \mathcal{D} \subset \mathbb{R}^P, t^k \in [0,T] \text{ evaluate } \\ |
\text{For } \mu \in \mathcal{D} \subset \mathbb{R}^P, t^k \in [0,T] \text{ evaluate } \\ |
||
| Line 132: | Line 131: | ||
To apply the offline-online decomposition, we assume they are affine parameter-dependent, i.e. |
To apply the offline-online decomposition, we assume they are affine parameter-dependent, i.e. |
||
| − | <math> |
+ | :<math> |
m(w,v;\mu) = \sum_{q=1}^{Q_m} \Theta_m^q(\mu,t) m^q(w,v) |
m(w,v;\mu) = \sum_{q=1}^{Q_m} \Theta_m^q(\mu,t) m^q(w,v) |
||
</math> |
</math> |
||
| − | <math> |
+ | :<math> |
a(w,v;\mu) = \sum_{q=1}^{Q_a} \Theta_a^q(\mu,t) a^q(w,v) |
a(w,v;\mu) = \sum_{q=1}^{Q_a} \Theta_a^q(\mu,t) a^q(w,v) |
||
</math> |
</math> |
||
| − | <math> |
+ | :<math> |
f(v;\mu) = \sum_{q=1}^{Q_f} \Theta_f^{q}(\mu,t) f^q(v). |
f(v;\mu) = \sum_{q=1}^{Q_f} \Theta_f^{q}(\mu,t) f^q(v). |
||
</math> |
</math> |
||
| Line 146: | Line 145: | ||
The Lagrange Reduced Basis space <math> V_N </math> is usually established by POD-Greedy algorithm <ref name="haasdonk08"/>. Then the input-output response can be presented as follows, through Galerkin projection, |
The Lagrange Reduced Basis space <math> V_N </math> is usually established by POD-Greedy algorithm <ref name="haasdonk08"/>. Then the input-output response can be presented as follows, through Galerkin projection, |
||
| − | <math> |
+ | :<math> |
\begin{cases} |
\begin{cases} |
||
\text{For } \mu \in \mathcal{D} \subset \mathbb{R}^P, t^k \in [0,T] \text{ evaluate } \\ |
\text{For } \mu \in \mathcal{D} \subset \mathbb{R}^P, t^k \in [0,T] \text{ evaluate } \\ |
||
Revision as of 00:13, 1 May 2013
Description
The Reduced Basis Method[1], [2] (RBM) we present here is applicable to static and time-dependent linear PDEs.
Time-Independent PDEs
The typical model problem of the RBM consists of a parametrized PDE stated in weak form with
bilinear form 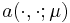 and linear form
and linear form 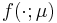 .
The parameter
.
The parameter 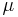 is considered within a domain
is considered within a domain 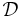 and we are interested in an output quantity
and we are interested in an output quantity 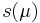 which can be
expressed via a linear functional
which can be
expressed via a linear functional 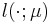 of the field variable
of the field variable 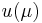 .
.
The exact, infinite-dimensional formulation, indicated by the superscript e, is given by
Through spatial discretization, e.g. finite element method, we consider the discretized system
The underlying assumption of the RBM is that the parametrically induced manifold 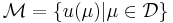 can be approximated by a low dimensional space
can be approximated by a low dimensional space 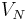 .
.
It also applies the concept of an offline-online decomposition, in that a large pre-processing offline cost is acceptable in view of a very low online cost (of a reduced order model) for each input-output evaluation, when in a many-query or real-time context.
The essential assumption which allows the offline-online decomposition is that there exists an affine parameter dependence
The Lagrange Reduced Basis space is established by iteratively choosing Lagrange parameter samples
and considering the associated Lagrange RB spaces
in a greedy sampling process. This leads to hierarchical RB spaces: 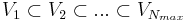 .
.
We then consider the galerkin projection onto the RB-space 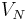
The greedy sampling uses an error estimator ot error indicator 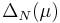 for the approximation error
for the approximation error 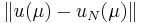 .
.
Steps of the greedy sampling process:
1. Let 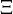 denote a finite sample of
denote a finite sample of 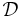 and set
and set 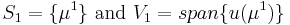 .
.
2. For 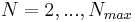 , find
, find 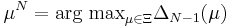 ,
,
3. Set 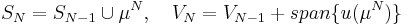 .
.
This method is used in the following models:
Time-Dependent PDEs
When time is involved, it can be roughly considered as an usual parameter just as time-independent case.
But more attention should be paid to the dynamics of the system and the stability is also a major concern,
especially for the nonlinear case. Mostly, we use the same notation as time-independent case except the
variable 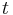 is added explicitly.
is added explicitly.
The exact, infinite-dimensional formulation, indicated by the superscript e, is given by
Here 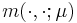 is also a bilinear form.
is also a bilinear form.
Assume a reference discretization form is given as follows,
The underlying assumption of the RBM is that the parametrically induced manifold 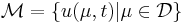 can be approximated by a low dimensional space
can be approximated by a low dimensional space 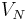 .
.
To apply the offline-online decomposition, we assume they are affine parameter-dependent, i.e.
The Lagrange Reduced Basis space 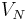 is usually established by POD-Greedy algorithm [3]. Then the input-output response can be presented as follows, through Galerkin projection,
is usually established by POD-Greedy algorithm [3]. Then the input-output response can be presented as follows, through Galerkin projection,
Note that the assumption of affine form can be relaxed in practice, then the empirical interpolation method [4] can be exploited for offline-online decomposition.
This method has been used for Batch Chromatography, where the empirical interpolation method was used for treating the nonaffinity.
References
- ↑ G. Rozza, D.B.P. Huynh, A.T. Patera, "Reduced Basis Approximation and a Posteriori Error Estimation for Affinely Parametrized Elliptic Coercive Partial Differential Equations", Arch Comput Methods Eng (2008) 15: 229–275.
- ↑ M. Grepl, "Reduced--basis approximations and posteriori error estimation for parabolic partial differential equations" PhD thesis, MIT, 2005.
- ↑ B. Haasdonk and M. Ohlberger, "Reduced basis method for finite volume approximations of parameterized linear evolution equations", Mathematical Modeling and Numerical Analysis, 42 (2008), 277-302.
- ↑ M. Barrault, Y. Maday, N.C. Nguyen, and A.T. Patera, "An 'empirical interpolation' method: application to efficient reduced-basis discretization of partial differential equations", C. R. Acad. Sci. Paris Series I, 339 (2004), 667-672.

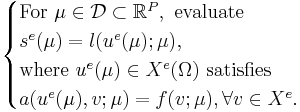
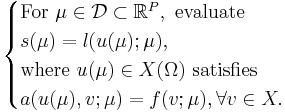
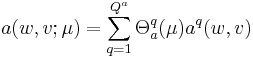
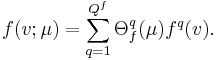
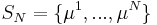
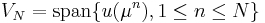
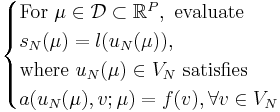
![\begin{cases}
\text{For } \mu \in \mathcal{D} \subset \mathbb{R}^P, t^k \in [0,T] \text{ evaluate } \\
s^e(\mu,t^k) = l(u^e(\mu,t);\mu), \\
\text{where } u^e(\mu,t) \in X^e(\Omega) \text{ satisfies } \\
m(u^e(\mu,t^k),v;\mu) + \Delta t a(u^e(\mu,t^k),v;\mu) = m(u^e(\mu,t^{k-1}),v;\mu) +
\Delta t f(v;\mu)u^e(\mu, t^k), \forall v \in X^e.
\end{cases}](/morwiki/images/math/2/5/0/2502798f3c978338082400fb691a0665.png)
![\begin{cases}
\text{For } \mu \in \mathcal{D} \subset \mathbb{R}^P, t^k \in [0,T] \text{ evaluate } \\
s(\mu,t^k) = l(u(\mu,t);\mu), \\
\text{where } u(\mu,t) \in X_{\mathcal N}(\Omega) \text{ satisfies } \\
m(u(\mu,t^k),v;\mu) + \Delta t a(u(\mu,t^k),v;\mu) = m(u(\mu,t^{k-1}),v;\mu) +
\Delta t f(v;\mu)u(\mu, t^k), \forall v \in X_{\mathcal N}.
\end{cases}](/morwiki/images/math/d/0/f/d0f1d97968db096c9a45f2dbe5d4f2f4.png)
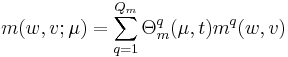
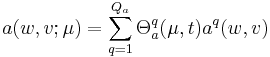
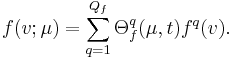
![\begin{cases}
\text{For } \mu \in \mathcal{D} \subset \mathbb{R}^P, t^k \in [0,T] \text{ evaluate } \\
s(\mu,t^k) = l(u_N(\mu,t);\mu), \\
\text{where } u_N(\mu,t) \in X_{N}(\Omega) \text{ satisfies } \\
m(u_N(\mu,t^k),v;\mu) + \Delta t a(u_N(\mu,t^k),v;\mu) = m(u_N(\mu,t^{k-1}),v;\mu) +
\Delta t f(v;\mu)u_N(\mu, t^k), \forall v \in X_N.
\end{cases}](/morwiki/images/math/1/9/a/19a97ba9278022a2f27e68901a50b082.png)