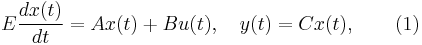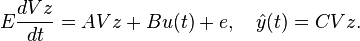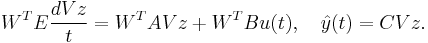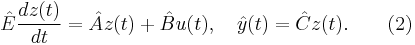m (remove link) |
|||
| (33 intermediate revisions by 6 users not shown) | |||
| Line 1: | Line 1: | ||
[[Category:method]] |
[[Category:method]] |
||
| + | [[Category:time invariant]] |
||
| + | Consider the linear time invariant system |
||
| ⚫ | |||
| − | All the existing model order reduction (MOR) methods are based on projection. That is to |
||
| ⚫ | |||
| − | find a subspace <math>S_1</math> which approximates the manifold where the state |
||
| + | y(t)=Cx(t), \quad \quad (1) |
||
| − | vector <math>x(t)</math> resides. Afterwards, <math>x(t)</math> is approximated by a vector <math>\tilde x(t)</math> in <math>S_1</math>. The reduced model is produced by Petrov-Galerkin projection onto a subspace <math>S_2</math>, or by Galerkin projection onto the same subspace <math>S_1</math>. |
||
| − | |||
| − | We use the system |
||
| − | |||
| ⚫ | |||
| ⚫ | |||
| − | <math> |
||
| − | y(t)=Cx(t), |
||
</math> |
</math> |
||
| − | as an example |
+ | as an example. |
| + | All the existing model order reduction (MOR) methods are based on projection<ref>Antoulas, A. C. "<span class="plainlinks">[http://dx.doi.org/10.1137/1.9780898718713 Approximation of large-scale dynamical systems]</span>". Vol. 6. Society for Industrial and Applied Mathematics, pp.376--377, 2009; ISBN 978-0-89871-529-3</ref>. |
||
| − | basis <math>V=(v_1,v_2, \ldots, v_q)</math> of the subspace <math>S_1</math> has been |
||
| − | + | That is to find a subspace <math>S_1</math> which approximates the manifold where the state vector <math>x(t)</math> resides. |
|
| − | + | Afterwards, <math>x(t)</math> is approximated by its projection <math>\hat x(t)</math> in <math>S_1</math>. |
|
| + | The reduced model is produced by [[wikipedia:Petrov–Galerkin_method|Petrov-Galerkin projection]] using a test subspace <math>S_2</math>, or by [[wikipedia:Galerkin_method|Galerkin projection]] using <math>S_1</math> as the test subspace. |
||
| − | of length <math>q \ll n</math>. |
||
| + | Assuming that an orthonormal basis <math>V=(v_1,v_2, \ldots, v_q)</math> of the subspace <math>S_1</math> has been found, then the approximation <math>\hat x(t)</math> in <math>S_1</math> can be represented by the basis as <math>\hat{x} (t)=V z(t)</math>. |
||
| − | |||
| − | + | Therefore <math>x(t)</math> can be approximated by <math> x(t) \approx V z(t)</math>. |
|
| − | + | Here <math>z</math> is a vector of length <math>q \ll n</math>. |
|
| + | Once <math>z(t)</math> is computed, an approximate solution <math>\hat x(t)=V z(t)</math> for <math>x(t)</math> can be obtained. |
||
| − | can be computed from the reduced model |
+ | The vector <math>z(t)</math> can be computed from the reduced model, derived by the following two steps. |
| − | following two steps. |
||
Step 1. By replacing <math>x</math> in (1) with <math>Vz</math>, we get |
Step 1. By replacing <math>x</math> in (1) with <math>Vz</math>, we get |
||
| − | <math>E \frac{d{Vz}}{dt} |
+ | :<math>E \frac{d{Vz}}{dt}=A Vz+Bu(t)+e,\quad \hat y(t)=CV z.</math> |
| − | <math>y(t) \approx CV z.</math> |
||
| − | Step 2. The residual is denoted as <math>e=AVz+Bu(t)-E \frac{d{Vz}}{dt}</math>. |
+ | Step 2. The residual is denoted as <math>e=AVz+Bu(t)-E \frac{d{Vz}}{dt}</math>. Forcing <math>e=0</math> in a properly chosen subspace <math>S_2</math> of <math>\mathbb {R}^n</math> leads to the Petrov-Galerkin projection: <math>W^T e=0</math>, where the columns of <math>W</math> are the basis of <math>S_2</math>. |
| + | Then we have, |
||
| − | <math>W^TE \frac{d{V z}}{t}=W^TA Vz +W^T B u(t),</math> |
+ | :<math>W^TE \frac{d{V z}}{t}=W^TA Vz +W^T B u(t), \quad \hat{y}(t)=CVz.</math> |
| − | <math>\hat{y}(t)=CVz.</math> |
||
By defining <math>\hat{E}=W^TEV</math>, <math>\hat {A}=W^TAV, \hat{B}=W^TB</math>, <math>\hat{C}=CV</math>, we get the final reduced model |
By defining <math>\hat{E}=W^TEV</math>, <math>\hat {A}=W^TAV, \hat{B}=W^TB</math>, <math>\hat{C}=CV</math>, we get the final reduced model |
||
| − | <math>\hat{E} \frac{dz(t)}{dt}=\hat{A}z(t)+\hat{B}u(t), |
+ | :<math>\hat{E} \frac{dz(t)}{dt}=\hat{A}z(t)+\hat{B}u(t), \quad |
| − | + | \hat{y}(t)=\hat{C}z(t). \quad \quad (2) |
|
</math> |
</math> |
||
| + | Notice that the approximation <math>\hat x(t)=Vz(t)</math> of <math>x(t)</math> can be obtained from <math> z(t)</math> by solving the system in (2). |
||
| − | Notice that the approximation <math>\hat x(t)=Vz(t)</math> of <math>x(t)</math> can be obtained from <math> z(t)</math> by solving the system in (3). The system in (3) is much smaller than the system in (1) in the sense that there are many less equations in (3) than in (1). Therefore, the system in (3) is much easier to be solved, which is the so-called reduced model. In order to save the simulation time of solving (1), reduced model can be used to replace (1) to attain a fast simulation. Furthermore, the error between the two systems should be within acceptable tolerance. The error can be measured through the error between the the state vectors <math>x(t), \hat x(t)</math>, or between the output responses <math>y(t), \hat y(t)</math>, or between the transfer functions of the two systems. |
||
| + | The system in (2) is much smaller than the system in (1) in the sense that there are many less equations in (2) than in (1). |
||
| − | |||
| + | Therefore, the system in (2) is much easier to be solved, which is the so-called reduced model. |
||
| ⚫ | |||
| + | In order to save the simulation time of solving (1), the reduced model can be used to replace (1) to attain a fast simulation. Furthermore, the error between the two systems should be within acceptable tolerance. |
||
| − | different from <math>V</math>, some methods use <math>W=V</math>, e.g. some of the moment matching MOR methods, the reduced basis methods, and some of the POD methods |
||
| + | The error can be measured through the error between the the state vectors <math>x(t), \hat x(t)</math>, or between the output responses <math>y(t), \hat y(t)</math>, or between the transfer functions of the two systems. |
||
| − | etc.. When <math>W=V</math>, Petrov-Galerkin projection becomes Galerkin |
||
| ⚫ | |||
| − | projection. |
||
| + | While the Gramian based MOR methods (e.g. [[Balanced Truncation]]) usually compute <math>W</math> different from <math>V</math>, some methods use <math>W=V</math>, e.g. some of the [[Moment-matching method]]s, the [[Reduced Basis PMOR method]]s, and some of the [[POD method]]s etc.. When <math>W=V</math>, Petrov-Galerkin projection becomes Galerkin projection. |
||
| − | |||
| − | MOR methods differ in the computation |
+ | MOR methods differ in the computation of the two matrices <math>W</math> and <math>V</math>. |
| − | + | The Gramian based MOR methods compute <math>W</math> and <math>V</math> by the controllability and observability Gramians. |
|
| ⚫ | Reduced basis methods and POD methods compute <math>V</math> from the snapshots of the state vector <math>x(t)</math> at different time steps (also at the samples of the parameters if the system is parametric). The methods based on moment-matching compute :<math>W</math> and <math>V</math> from the moments of the transfer function. |
||
| − | observability Gramians. Reduced |
||
| + | In eigenvalue based MOR methods, e.g. [[Modal truncation]], the columns of :<math>W</math> and <math>V</math> are eigenvectors or invariant subspaces corresponding to selected eigenvalues of the matrix pair <math>(A,E)</math>. |
||
| − | basis methods and POD methods compute <math>V</math> from the snapshots of the |
||
| ⚫ | |||
| − | <math>W</math> and <math>V</math> from the moments of the transfer function. |
||
| + | One common goal of all MOR methods is that the behavior of the reduced model should be sufficiently "close" to that of the original model guaranteed through the above mentioned error measurements. |
||
| − | One common |
||
| − | goal of all MOR methods is that the behavior of the reduced model |
||
| − | should be sufficiently "close" to that of the original model through certain error estimators. |
||
| + | ==References== |
||
| − | Contact information |
||
| + | <references/> |
||
| − | Lihong Feng |
||
Latest revision as of 13:24, 11 May 2023
Consider the linear time invariant system
as an example.
All the existing model order reduction (MOR) methods are based on projection[1].
That is to find a subspace 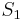 which approximates the manifold where the state vector
which approximates the manifold where the state vector 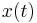 resides.
Afterwards,
resides.
Afterwards, 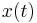 is approximated by its projection
is approximated by its projection 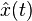 in
in 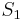 .
The reduced model is produced by Petrov-Galerkin projection using a test subspace
.
The reduced model is produced by Petrov-Galerkin projection using a test subspace 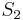 , or by Galerkin projection using
, or by Galerkin projection using 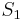 as the test subspace.
Assuming that an orthonormal basis
as the test subspace.
Assuming that an orthonormal basis 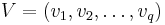 of the subspace
of the subspace 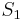 has been found, then the approximation
has been found, then the approximation 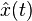 in
in 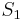 can be represented by the basis as
can be represented by the basis as 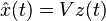 .
Therefore
.
Therefore 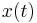 can be approximated by
can be approximated by 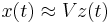 .
Here
.
Here 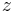 is a vector of length
is a vector of length 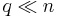 .
Once
.
Once 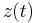 is computed, an approximate solution
is computed, an approximate solution 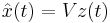 for
for 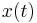 can be obtained.
The vector
can be obtained.
The vector 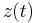 can be computed from the reduced model, derived by the following two steps.
can be computed from the reduced model, derived by the following two steps.
Step 1. By replacing  in (1) with
in (1) with 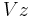 , we get
, we get
Step 2. The residual is denoted as 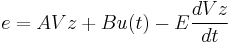 . Forcing
. Forcing 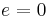 in a properly chosen subspace
in a properly chosen subspace 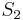 of
of 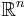 leads to the Petrov-Galerkin projection:
leads to the Petrov-Galerkin projection: 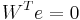 , where the columns of
, where the columns of 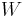 are the basis of
are the basis of 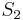 .
Then we have,
.
Then we have,
By defining 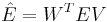 ,
, 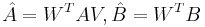 ,
, 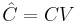 , we get the final reduced model
, we get the final reduced model
Notice that the approximation 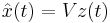 of
of 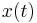 can be obtained from
can be obtained from 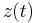 by solving the system in (2).
The system in (2) is much smaller than the system in (1) in the sense that there are many less equations in (2) than in (1).
Therefore, the system in (2) is much easier to be solved, which is the so-called reduced model.
In order to save the simulation time of solving (1), the reduced model can be used to replace (1) to attain a fast simulation. Furthermore, the error between the two systems should be within acceptable tolerance.
The error can be measured through the error between the the state vectors
by solving the system in (2).
The system in (2) is much smaller than the system in (1) in the sense that there are many less equations in (2) than in (1).
Therefore, the system in (2) is much easier to be solved, which is the so-called reduced model.
In order to save the simulation time of solving (1), the reduced model can be used to replace (1) to attain a fast simulation. Furthermore, the error between the two systems should be within acceptable tolerance.
The error can be measured through the error between the the state vectors 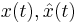 , or between the output responses
, or between the output responses 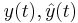 , or between the transfer functions of the two systems.
It can be seen that once the two matrices
, or between the transfer functions of the two systems.
It can be seen that once the two matrices 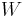 and
and 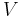 have been computed, the reduced model is obtained.
While the Gramian based MOR methods (e.g. Balanced Truncation) usually compute
have been computed, the reduced model is obtained.
While the Gramian based MOR methods (e.g. Balanced Truncation) usually compute 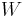 different from
different from 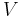 , some methods use
, some methods use 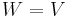 , e.g. some of the Moment-matching methods, the Reduced Basis PMOR methods, and some of the POD methods etc.. When
, e.g. some of the Moment-matching methods, the Reduced Basis PMOR methods, and some of the POD methods etc.. When 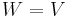 , Petrov-Galerkin projection becomes Galerkin projection.
MOR methods differ in the computation of the two matrices
, Petrov-Galerkin projection becomes Galerkin projection.
MOR methods differ in the computation of the two matrices 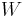 and
and 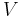 .
The Gramian based MOR methods compute
.
The Gramian based MOR methods compute 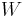 and
and 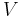 by the controllability and observability Gramians.
Reduced basis methods and POD methods compute
by the controllability and observability Gramians.
Reduced basis methods and POD methods compute 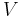 from the snapshots of the state vector
from the snapshots of the state vector 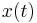 at different time steps (also at the samples of the parameters if the system is parametric). The methods based on moment-matching compute :
at different time steps (also at the samples of the parameters if the system is parametric). The methods based on moment-matching compute :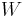 and
and 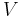 from the moments of the transfer function.
In eigenvalue based MOR methods, e.g. Modal truncation, the columns of :
from the moments of the transfer function.
In eigenvalue based MOR methods, e.g. Modal truncation, the columns of :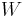 and
and 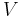 are eigenvectors or invariant subspaces corresponding to selected eigenvalues of the matrix pair
are eigenvectors or invariant subspaces corresponding to selected eigenvalues of the matrix pair 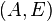 .
.
One common goal of all MOR methods is that the behavior of the reduced model should be sufficiently "close" to that of the original model guaranteed through the above mentioned error measurements.
References
- ↑ Antoulas, A. C. "Approximation of large-scale dynamical systems". Vol. 6. Society for Industrial and Applied Mathematics, pp.376--377, 2009; ISBN 978-0-89871-529-3