| (16 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
[[Category:method]] |
[[Category:method]] |
||
| − | [[Category:parametric |
+ | [[Category:parametric]] |
| + | ==Description== |
||
| ⚫ | |||
| + | |||
| ⚫ | |||
==Time-Independent PDEs== |
==Time-Independent PDEs== |
||
| Line 14: | Line 16: | ||
The exact, infinite-dimensional formulation, indicated by the superscript e, is given by |
The exact, infinite-dimensional formulation, indicated by the superscript e, is given by |
||
| ⚫ | |||
| − | |||
| ⚫ | |||
\begin{cases} |
\begin{cases} |
||
\text{For } \mu \in \mathcal{D} \subset \mathbb{R}^P, \text{ evaluate } \\ |
\text{For } \mu \in \mathcal{D} \subset \mathbb{R}^P, \text{ evaluate } \\ |
||
| Line 26: | Line 27: | ||
Through spatial discretization, e.g. finite element method, we consider the discretized system |
Through spatial discretization, e.g. finite element method, we consider the discretized system |
||
| − | <math> |
+ | :<math> |
\begin{cases} |
\begin{cases} |
||
\text{For } \mu \in \mathcal{D} \subset \mathbb{R}^P, \text{ evaluate } \\ |
\text{For } \mu \in \mathcal{D} \subset \mathbb{R}^P, \text{ evaluate } \\ |
||
| Line 43: | Line 44: | ||
The essential assumption which allows the offline-online decomposition is that there exists an affine parameter dependence |
The essential assumption which allows the offline-online decomposition is that there exists an affine parameter dependence |
||
| − | <math> |
+ | :<math> |
a(w,v;\mu) = \sum_{q=1}^{Q^a} \Theta_a^q(\mu) a^q(w,v) |
a(w,v;\mu) = \sum_{q=1}^{Q^a} \Theta_a^q(\mu) a^q(w,v) |
||
</math> |
</math> |
||
| − | <math> |
+ | :<math> |
f(v;\mu) = \sum_{q=1}^{Q^f} \Theta_f^{q}(\mu) f^q(v). |
f(v;\mu) = \sum_{q=1}^{Q^f} \Theta_f^{q}(\mu) f^q(v). |
||
</math> |
</math> |
||
| Line 53: | Line 54: | ||
The Lagrange Reduced Basis space is established by iteratively choosing Lagrange parameter samples |
The Lagrange Reduced Basis space is established by iteratively choosing Lagrange parameter samples |
||
| − | <math> |
+ | :<math> |
S_N = \{\mu^1,...,\mu^N\} |
S_N = \{\mu^1,...,\mu^N\} |
||
</math> |
</math> |
||
| Line 59: | Line 60: | ||
and considering the associated Lagrange RB spaces |
and considering the associated Lagrange RB spaces |
||
| − | <math> |
+ | :<math> |
V_N = \text{span}\{u(\mu^n), 1 \leq n \leq N \} |
V_N = \text{span}\{u(\mu^n), 1 \leq n \leq N \} |
||
</math> |
</math> |
||
| Line 67: | Line 68: | ||
We then consider the galerkin projection onto the RB-space <math> V_N </math> |
We then consider the galerkin projection onto the RB-space <math> V_N </math> |
||
| − | <math> |
+ | :<math> |
\begin{cases} |
\begin{cases} |
||
\text{For } \mu \in \mathcal{D} \subset \mathbb{R}^P, \text{ evaluate } \\ |
\text{For } \mu \in \mathcal{D} \subset \mathbb{R}^P, \text{ evaluate } \\ |
||
| Line 76: | Line 77: | ||
</math> |
</math> |
||
| − | The greedy sampling uses an error estimator <math> \Delta_{N}(\mu) </math> |
+ | The greedy sampling uses an error estimator ot error indicator <math> \Delta_{N}(\mu) </math> for the approximation error <math> \| u(\mu) - u_N(\mu) \| </math>. |
| − | + | Steps of the greedy sampling process: |
|
1. Let <math> \Xi </math> denote a finite sample of <math> \mathcal{D} </math> and set <math> S_1 = \{\mu^1\} \text{ and } V_1 = span\{ u(\mu^1) \} </math>. |
1. Let <math> \Xi </math> denote a finite sample of <math> \mathcal{D} </math> and set <math> S_1 = \{\mu^1\} \text{ and } V_1 = span\{ u(\mu^1) \} </math>. |
||
| Line 85: | Line 86: | ||
3. Set <math> S_N = S_{N-1} \cup \mu^N , \quad V_N = V_{N-1} + span\{u(\mu^N)\} </math>. |
3. Set <math> S_N = S_{N-1} \cup \mu^N , \quad V_N = V_{N-1} + span\{u(\mu^N)\} </math>. |
||
| + | |||
| + | This method is used in the following models: |
||
| + | |||
| + | [[Coplanar_Waveguide]] |
||
| + | |||
| + | [[Branchline Coupler]] |
||
==Time-Dependent PDEs== |
==Time-Dependent PDEs== |
||
| Line 95: | Line 102: | ||
The exact, infinite-dimensional formulation, indicated by the superscript e, is given by |
The exact, infinite-dimensional formulation, indicated by the superscript e, is given by |
||
| − | <math> |
+ | :<math> |
\begin{cases} |
\begin{cases} |
||
\text{For } \mu \in \mathcal{D} \subset \mathbb{R}^P, t^k \in [0,T] \text{ evaluate } \\ |
\text{For } \mu \in \mathcal{D} \subset \mathbb{R}^P, t^k \in [0,T] \text{ evaluate } \\ |
||
| Line 109: | Line 116: | ||
Assume a reference discretization form is given as follows, |
Assume a reference discretization form is given as follows, |
||
| − | <math> |
+ | :<math> |
\begin{cases} |
\begin{cases} |
||
\text{For } \mu \in \mathcal{D} \subset \mathbb{R}^P, t^k \in [0,T] \text{ evaluate } \\ |
\text{For } \mu \in \mathcal{D} \subset \mathbb{R}^P, t^k \in [0,T] \text{ evaluate } \\ |
||
| Line 124: | Line 131: | ||
To apply the offline-online decomposition, we assume they are affine parameter-dependent, i.e. |
To apply the offline-online decomposition, we assume they are affine parameter-dependent, i.e. |
||
| − | <math> |
+ | :<math> |
m(w,v;\mu) = \sum_{q=1}^{Q_m} \Theta_m^q(\mu,t) m^q(w,v) |
m(w,v;\mu) = \sum_{q=1}^{Q_m} \Theta_m^q(\mu,t) m^q(w,v) |
||
</math> |
</math> |
||
| − | <math> |
+ | :<math> |
a(w,v;\mu) = \sum_{q=1}^{Q_a} \Theta_a^q(\mu,t) a^q(w,v) |
a(w,v;\mu) = \sum_{q=1}^{Q_a} \Theta_a^q(\mu,t) a^q(w,v) |
||
</math> |
</math> |
||
| − | <math> |
+ | :<math> |
f(v;\mu) = \sum_{q=1}^{Q_f} \Theta_f^{q}(\mu,t) f^q(v). |
f(v;\mu) = \sum_{q=1}^{Q_f} \Theta_f^{q}(\mu,t) f^q(v). |
||
</math> |
</math> |
||
| − | The Lagrange Reduced Basis space <math> V_N </math> is usually established by POD-Greedy algorithm |
+ | The Lagrange Reduced Basis space <math> V_N </math> is usually established by POD-Greedy algorithm <ref name="haasdonk08"/>. Then the input-output response can be presented as follows, through Galerkin projection, |
| − | Then the input-output response can present as follows, with Galerkin projection, |
||
| − | <math> |
+ | :<math> |
\begin{cases} |
\begin{cases} |
||
\text{For } \mu \in \mathcal{D} \subset \mathbb{R}^P, t^k \in [0,T] \text{ evaluate } \\ |
\text{For } \mu \in \mathcal{D} \subset \mathbb{R}^P, t^k \in [0,T] \text{ evaluate } \\ |
||
| Line 149: | Line 155: | ||
</math> |
</math> |
||
| − | Note that the assumption of affine form can be relaxed in practice, then empirical interpolation |
+ | Note that the assumption of affine form can be relaxed in practice, then the empirical interpolation method <ref name="barrault04"/> can be exploited for |
offline-online decomposition. |
offline-online decomposition. |
||
| + | |||
| + | This method has been used for [[Batch_Chromatography|Batch Chromatography]], where the empirical interpolation method was used for treating the nonaffinity. |
||
==References== |
==References== |
||
| − | [1] M. Barrault, Y. Maday, N. Nguyen, and A. Patera, |
||
| − | An `empirical interpolation' method: application |
||
| − | to effcient reduced-basis discretization of partial differential equations, |
||
| − | C. R. Math. Acad. Sci. Paris Series I, 339 (2004), 667-672. |
||
| + | <references> |
||
| − | [2] M. Grepl, |
||
| + | |||
| ⚫ | |||
| + | <ref name="barrault04"> M. Barrault, Y. Maday, N.C. Nguyen, and A.T. Patera, "<span class="plainlinks">[http://dx.doi.org/10.1016/j.crma.2004.08.006 An 'empirical interpolation' method: application to efficient reduced-basis discretization of partial differential equations]</span>", C. R. Acad. Sci. Paris Series I, 339 (2004), 667-672.</ref> |
||
| − | PhD thesis, MIT, 2005. |
||
| ⚫ | |||
| − | [3] B. Haasdonk and M. Ohlberger, |
||
| − | Reduced basis method for finite volume approximations of parameterized linear evolution equations, |
||
| − | Mathematical Modeling and Numerical Analysis, 42 (2008), 277-302. |
||
| + | <ref name="haasdonk08"> B. Haasdonk and M. Ohlberger, "<span class="plainlinks">[http://www.agh.ians.uni-stuttgart.de/publications/2008/HO08b Reduced basis method for finite volume approximations of parameterized linear evolution equations]</span>", Mathematical Modeling and Numerical Analysis, 42 (2008), 277-302.</ref> |
||
| − | [4] G. Rozza, D.B.P. Huynh, A.T. Patera |
||
| ⚫ | |||
| − | Arch Comput Methods Eng (2008) 15: 229–275. |
||
| ⚫ | <ref name="rozza08">G. Rozza, D.B.P. Huynh, A.T. Patera, "<span class="plainlinks">[http://dx.doi.org/10.1007/s11831-008-9019-9 Reduced Basis Approximation and a Posteriori Error Estimation for Affinely Parametrized Elliptic Coercive Partial Differential Equations]</span>", Arch Comput Methods Eng (2008) 15: 229–275.</ref> |
||
| + | </references> |
||
| − | Contact |
+ | ==Contact== |
'' [[User:hessm|Martin Hess]]'' |
'' [[User:hessm|Martin Hess]]'' |
||
Latest revision as of 08:58, 23 May 2013
Description
The Reduced Basis Method[1], [2] (RBM) we present here is a Projection based MOR method, applicable to static and time-dependent linear PDEs.
Time-Independent PDEs
The typical model problem of the RBM consists of a parametrized PDE stated in weak form with
bilinear form 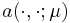 and linear form
and linear form 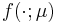 .
The parameter
.
The parameter 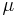 is considered within a domain
is considered within a domain 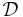 and we are interested in an output quantity
and we are interested in an output quantity 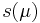 which can be
expressed via a linear functional
which can be
expressed via a linear functional 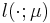 of the field variable
of the field variable 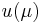 .
.
The exact, infinite-dimensional formulation, indicated by the superscript e, is given by
Through spatial discretization, e.g. finite element method, we consider the discretized system
The underlying assumption of the RBM is that the parametrically induced manifold 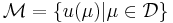 can be approximated by a low dimensional space
can be approximated by a low dimensional space 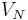 .
.
It also applies the concept of an offline-online decomposition, in that a large pre-processing offline cost is acceptable in view of a very low online cost (of a reduced order model) for each input-output evaluation, when in a many-query or real-time context.
The essential assumption which allows the offline-online decomposition is that there exists an affine parameter dependence
The Lagrange Reduced Basis space is established by iteratively choosing Lagrange parameter samples
and considering the associated Lagrange RB spaces
in a greedy sampling process. This leads to hierarchical RB spaces: 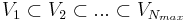 .
.
We then consider the galerkin projection onto the RB-space 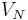
The greedy sampling uses an error estimator ot error indicator 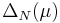 for the approximation error
for the approximation error 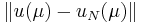 .
.
Steps of the greedy sampling process:
1. Let 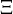 denote a finite sample of
denote a finite sample of 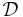 and set
and set 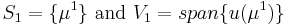 .
.
2. For 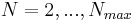 , find
, find 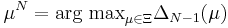 ,
,
3. Set 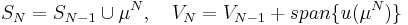 .
.
This method is used in the following models:
Time-Dependent PDEs
When time is involved, it can be roughly considered as an usual parameter just as time-independent case.
But more attention should be paid to the dynamics of the system and the stability is also a major concern,
especially for the nonlinear case. Mostly, we use the same notation as time-independent case except the
variable 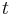 is added explicitly.
is added explicitly.
The exact, infinite-dimensional formulation, indicated by the superscript e, is given by
Here 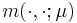 is also a bilinear form.
is also a bilinear form.
Assume a reference discretization form is given as follows,
The underlying assumption of the RBM is that the parametrically induced manifold 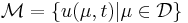 can be approximated by a low dimensional space
can be approximated by a low dimensional space 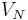 .
.
To apply the offline-online decomposition, we assume they are affine parameter-dependent, i.e.
The Lagrange Reduced Basis space 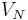 is usually established by POD-Greedy algorithm [3]. Then the input-output response can be presented as follows, through Galerkin projection,
is usually established by POD-Greedy algorithm [3]. Then the input-output response can be presented as follows, through Galerkin projection,
Note that the assumption of affine form can be relaxed in practice, then the empirical interpolation method [4] can be exploited for offline-online decomposition.
This method has been used for Batch Chromatography, where the empirical interpolation method was used for treating the nonaffinity.
References
- ↑ G. Rozza, D.B.P. Huynh, A.T. Patera, "Reduced Basis Approximation and a Posteriori Error Estimation for Affinely Parametrized Elliptic Coercive Partial Differential Equations", Arch Comput Methods Eng (2008) 15: 229–275.
- ↑ M. Grepl, "Reduced--basis approximations and posteriori error estimation for parabolic partial differential equations" PhD thesis, MIT, 2005.
- ↑ B. Haasdonk and M. Ohlberger, "Reduced basis method for finite volume approximations of parameterized linear evolution equations", Mathematical Modeling and Numerical Analysis, 42 (2008), 277-302.
- ↑ M. Barrault, Y. Maday, N.C. Nguyen, and A.T. Patera, "An 'empirical interpolation' method: application to efficient reduced-basis discretization of partial differential equations", C. R. Acad. Sci. Paris Series I, 339 (2004), 667-672.

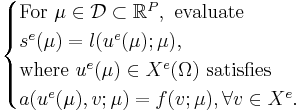
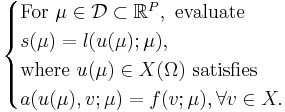
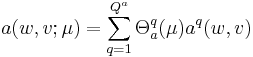
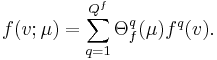
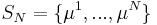
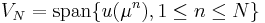
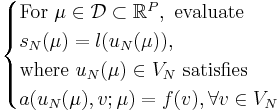
![\begin{cases}
\text{For } \mu \in \mathcal{D} \subset \mathbb{R}^P, t^k \in [0,T] \text{ evaluate } \\
s^e(\mu,t^k) = l(u^e(\mu,t);\mu), \\
\text{where } u^e(\mu,t) \in X^e(\Omega) \text{ satisfies } \\
m(u^e(\mu,t^k),v;\mu) + \Delta t a(u^e(\mu,t^k),v;\mu) = m(u^e(\mu,t^{k-1}),v;\mu) +
\Delta t f(v;\mu)u^e(\mu, t^k), \forall v \in X^e.
\end{cases}](/morwiki/images/math/2/5/0/2502798f3c978338082400fb691a0665.png)
![\begin{cases}
\text{For } \mu \in \mathcal{D} \subset \mathbb{R}^P, t^k \in [0,T] \text{ evaluate } \\
s(\mu,t^k) = l(u(\mu,t);\mu), \\
\text{where } u(\mu,t) \in X_{\mathcal N}(\Omega) \text{ satisfies } \\
m(u(\mu,t^k),v;\mu) + \Delta t a(u(\mu,t^k),v;\mu) = m(u(\mu,t^{k-1}),v;\mu) +
\Delta t f(v;\mu)u(\mu, t^k), \forall v \in X_{\mathcal N}.
\end{cases}](/morwiki/images/math/d/0/f/d0f1d97968db096c9a45f2dbe5d4f2f4.png)
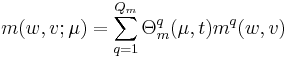
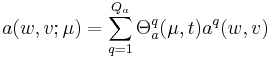
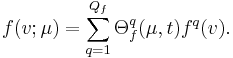
![\begin{cases}
\text{For } \mu \in \mathcal{D} \subset \mathbb{R}^P, t^k \in [0,T] \text{ evaluate } \\
s(\mu,t^k) = l(u_N(\mu,t);\mu), \\
\text{where } u_N(\mu,t) \in X_{N}(\Omega) \text{ satisfies } \\
m(u_N(\mu,t^k),v;\mu) + \Delta t a(u_N(\mu,t^k),v;\mu) = m(u_N(\mu,t^{k-1}),v;\mu) +
\Delta t f(v;\mu)u_N(\mu, t^k), \forall v \in X_N.
\end{cases}](/morwiki/images/math/1/9/a/19a97ba9278022a2f27e68901a50b082.png)