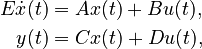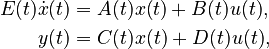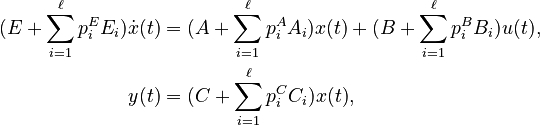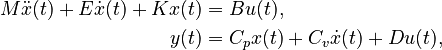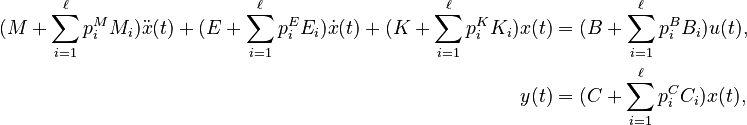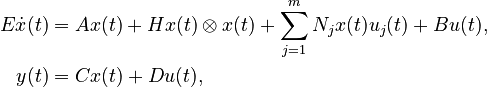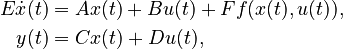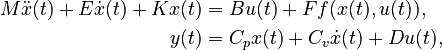m (fix missed M dimensions) |
|||
| (30 intermediate revisions by one other user not shown) | |||
| Line 1: | Line 1: | ||
| ⚫ | |||
| − | {{preliminary}} <!-- Do not remove --> |
||
| ⚫ | |||
| ⚫ | |||
| + | This page specifies templates for the types of models used as benchmark systems. In particular, the naming schemes established here are used in the corresponding data sets for all benchmarks. For example, <math>A</math> always serves as the name of the component matrix applied to the state <math>x(t)</math> in a linear time-invariant, first-order system. |
||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| + | For all parametric models, we assume each component has <math>\ell</math> parameters; in cases where a component has fewer than <math>\ell</math> parameters, the extras are treated as <math>0</math>. |
||
| + | Some benchmarks (e.g., [[Bone Model]]) have a constant forcing term, in which case, it is assumed that <math>u(t)</math> is identically <math>1</math>. |
||
| ⚫ | |||
| ⚫ | |||
| − | This page outlines the types of models that are used as benchmark systems. |
||
| ⚫ | |||
| ⚫ | |||
| − | |||
| ⚫ | |||
:<math> |
:<math> |
||
\begin{align} |
\begin{align} |
||
E\dot{x}(t) &= Ax(t) + Bu(t),\\ |
E\dot{x}(t) &= Ax(t) + Bu(t),\\ |
||
| − | y(t) &= Cx(t), |
+ | y(t) &= Cx(t) + Du(t), |
\end{align} |
\end{align} |
||
</math> |
</math> |
||
| − | with |
+ | with |
<math>E \in \mathbb{R}^{n \times n}</math>, |
<math>E \in \mathbb{R}^{n \times n}</math>, |
||
<math>A \in \mathbb{R}^{n \times n}</math>, |
<math>A \in \mathbb{R}^{n \times n}</math>, |
||
<math>B \in \mathbb{R}^{n \times m}</math>, |
<math>B \in \mathbb{R}^{n \times m}</math>, |
||
| − | <math>C \in \mathbb{R}^{q \times n}</math> |
+ | <math>C \in \mathbb{R}^{q \times n}</math>, |
| ⚫ | |||
| + | By default <math>E = I</math> and <math>D = 0</math>, unless explicitly provided. |
||
| − | ===Linear Time-Varying System=== |
+ | ===Linear Time-Varying First-Order System (LTV-FOS)=== |
:<math> |
:<math> |
||
\begin{align} |
\begin{align} |
||
E(t)\dot{x}(t) &= A(t)x(t) + B(t)u(t),\\ |
E(t)\dot{x}(t) &= A(t)x(t) + B(t)u(t),\\ |
||
| − | y(t) &= C(t)x(t), |
+ | y(t) &= C(t)x(t) + D(t)u(t), |
\end{align} |
\end{align} |
||
</math> |
</math> |
||
| − | with |
+ | with |
<math>E : \mathbb{R} \to \mathbb{R}^{n \times n}</math>, |
<math>E : \mathbb{R} \to \mathbb{R}^{n \times n}</math>, |
||
<math>A : \mathbb{R} \to \mathbb{R}^{n \times n}</math>, |
<math>A : \mathbb{R} \to \mathbb{R}^{n \times n}</math>, |
||
<math>B : \mathbb{R} \to \mathbb{R}^{n \times m}</math>, |
<math>B : \mathbb{R} \to \mathbb{R}^{n \times m}</math>, |
||
| − | <math>C : \mathbb{R} \to \mathbb{R}^{q \times n}</math> |
+ | <math>C : \mathbb{R} \to \mathbb{R}^{q \times n}</math>, |
| ⚫ | |||
| + | By default <math>E = I</math> and <math>D = 0</math>, unless explicitly provided. |
||
| ⚫ | |||
| ⚫ | |||
:<math> |
:<math> |
||
\begin{align} |
\begin{align} |
||
| − | + | (E + \sum_{i=1}^{\ell} p^E_i E_i)\dot{x}(t) &= (A + \sum_{i=1}^{\ell} p^A_i A_i) x(t) + (B + \sum_{i=1}^{\ell} p^B_i B_i)u(t),\\ |
|
| − | + | y(t) &= (C + \sum_{i=1}^{\ell} p^C_i C_i)x(t), |
|
\end{align} |
\end{align} |
||
</math> |
</math> |
||
| − | with |
+ | with |
| − | <math>E \in \mathbb{R}^{n \times n}</math> |
+ | <math>E, E_i \in \mathbb{R}^{n \times n}</math>; |
| − | <math>A \in \mathbb{R}^{n \times n}</math> |
+ | <math>A, A_i \in \mathbb{R}^{n \times n}</math>; |
| − | <math> |
+ | <math>B, B_i \in \mathbb{R}^{n \times m}</math>; and |
| − | <math> |
+ | <math>C, C_i \in \mathbb{R}^{q \times n}</math>, |
| − | <math> |
+ | for all <math>i = 1, \ldots, \ell</math>. |
| ⚫ | |||
| ⚫ | |||
| + | By default <math>E = I, E_i = 0</math>, unless explicitly provided. If <math>A_i</math> are provided without <math>A</math>, then it is assumed <math>A = 0</math>. Likewise for <math>B</math>, <math>C</math>, and <math>E</math>. |
||
| ⚫ | |||
| + | |||
| + | ===Linear Time-Invariant Second-Order System (LTI-SOS)=== |
||
:<math> |
:<math> |
||
\begin{align} |
\begin{align} |
||
| − | + | M \ddot{x}(t) + E \dot{x}(t) + K x(t) &= B u(t), \\ |
|
| − | y(t) &= |
+ | y(t) &= C_p x(t) + C_v \dot{x}(t) + D u(t), |
\end{align} |
\end{align} |
||
</math> |
</math> |
||
| − | with |
+ | with |
| ⚫ | |||
<math>E \in \mathbb{R}^{n \times n}</math>, |
<math>E \in \mathbb{R}^{n \times n}</math>, |
||
| − | <math> |
+ | <math>K \in \mathbb{R}^{n \times n}</math>, |
<math>B \in \mathbb{R}^{n \times m}</math>, |
<math>B \in \mathbb{R}^{n \times m}</math>, |
||
| − | <math> |
+ | <math>C_p, C_v \in \mathbb{R}^{q \times n}</math>, |
| − | <math> |
+ | <math>D \in \mathbb{R}^{q \times m}</math>. |
| + | When <math>C_v = 0</math>, we denote <math>C = C_p</math>. By default <math>E = I</math> and <math>D = 0</math>, unless explicitly provided. |
||
| − | ===Affine |
+ | ===Affine-Parametric LTI-SOS (AP-LTI-SOS)=== |
:<math> |
:<math> |
||
\begin{align} |
\begin{align} |
||
| − | ( |
+ | (M + \sum_{i=1}^{\ell} p^M_i M_i)\ddot{x}(t) + (E + \sum_{i=1}^{\ell} p^E_i E_i)\dot{x}(t) + (K + \sum_{i=1}^{\ell} p^K_i K_i)x(t) &= (B + \sum_{i=1}^{\ell} p^B_i B_i) u(t), \\ |
| − | y(t) &= |
+ | y(t) &= (C + \sum_{i=1}^{\ell} p^C_i C_i) x(t), |
\end{align} |
\end{align} |
||
</math> |
</math> |
||
| − | with |
+ | with |
| − | <math> |
+ | <math>M, M_i \in \mathbb{R}^{n \times n}</math>; |
| − | <math> |
+ | <math>E, E_i \in \mathbb{R}^{n \times n}</math>; |
| − | <math> |
+ | <math>K, K_i \in \mathbb{R}^{n \times n}</math>; |
| − | <math> |
+ | <math>B, B_i \in \mathbb{R}^{n \times m}</math>; and |
| − | <math> |
+ | <math>C, C_i \in \mathbb{R}^{q \times n}</math>, |
| − | <math> |
+ | for all <math>i = 1, \ldots, \ell</math>. |
| + | By default <math>E = I, E_i = 0</math>, unless explicitly provided. If <math>M_i</math> are provided without <math>M</math>, then it is assumed <math>M = 0</math>. Likewise for <math>K</math>, <math>B</math>, and <math>C</math>. |
||
| ⚫ | |||
| + | |||
| ⚫ | |||
:<math> |
:<math> |
||
\begin{align} |
\begin{align} |
||
| − | + | E\dot{x}(t) &= A x(t) + H x(t) \otimes x(t) + \sum_{j=1}^m N_j x(t) u_j(t) + B u(t), \\ |
|
| − | y(t) &= |
+ | y(t) &= Cx(t) + Du(t), |
\end{align} |
\end{align} |
||
</math> |
</math> |
||
| − | with |
+ | with |
| ⚫ | |||
<math>E \in \mathbb{R}^{n \times n}</math>, |
<math>E \in \mathbb{R}^{n \times n}</math>, |
||
| − | <math> |
+ | <math>A \in \mathbb{R}^{n \times n}</math>, |
| ⚫ | |||
| ⚫ | |||
<math>B \in \mathbb{R}^{n \times m}</math>, |
<math>B \in \mathbb{R}^{n \times m}</math>, |
||
| − | <math>C \in \mathbb{R}^{q \times n}</math> |
+ | <math>C \in \mathbb{R}^{q \times n}</math>, |
| ⚫ | |||
| − | ===Nonlinear |
+ | ===Nonlinear Time-Invariant First-Order System (NLTI-FOS)=== |
:<math> |
:<math> |
||
\begin{align} |
\begin{align} |
||
| − | + | E\dot{x}(t) &= Ax(t) + Bu(t) + F f(x(t),u(t)),\\ |
|
| − | y(t) &= |
+ | y(t) &= Cx(t) + Du(t), |
\end{align} |
\end{align} |
||
</math> |
</math> |
||
| − | with |
+ | with |
| ⚫ | |||
<math>E \in \mathbb{R}^{n \times n}</math>, |
<math>E \in \mathbb{R}^{n \times n}</math>, |
||
| − | <math> |
+ | <math>A \in \mathbb{R}^{n \times n}</math>, |
<math>B \in \mathbb{R}^{n \times m}</math>, |
<math>B \in \mathbb{R}^{n \times m}</math>, |
||
<math>C \in \mathbb{R}^{q \times n}</math>, |
<math>C \in \mathbb{R}^{q \times n}</math>, |
||
| + | <math>D \in \mathbb{R}^{q \times m}</math>, |
||
| + | <math>F \in \mathbb{R}^{n \times n}</math>, |
||
<math>f : \mathbb{R}^n \times \mathbb{R}^m \to \mathbb{R}^n</math>. |
<math>f : \mathbb{R}^n \times \mathbb{R}^m \to \mathbb{R}^n</math>. |
||
| + | By default <math>F = I</math>, <math>E = I</math>, <math>D = 0</math>, unless explicitly provided. |
||
| ⚫ | |||
| + | |||
| ⚫ | |||
:<math> |
:<math> |
||
\begin{align} |
\begin{align} |
||
| − | + | M \ddot{x}(t) + E \dot{x}(t) + K x(t) &= B u(t) + F f(x(t),u(t)), \\ |
|
| − | y(t) &= |
+ | y(t) &= C_p x(t) + C_v \dot{x}(t) + D u(t), |
\end{align} |
\end{align} |
||
</math> |
</math> |
||
| − | with |
+ | with |
| − | <math> |
+ | <math>M \in \mathbb{R}^{n \times n}</math>, |
| − | <math> |
+ | <math>E \in \mathbb{R}^{n \times n}</math>, |
| − | <math> |
+ | <math>K \in \mathbb{R}^{n \times n}</math>, |
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
<math>B \in \mathbb{R}^{n \times m}</math>, |
<math>B \in \mathbb{R}^{n \times m}</math>, |
||
| − | <math> |
+ | <math>F \in \mathbb{R}^{n \times n}</math>, |
| + | <math>C_p, C_v \in \mathbb{R}^{q \times n}</math>, |
||
| + | <math>D \in \mathbb{R}^{q \times m}</math>, |
||
| + | <math>f : \mathbb{R}^n \times \mathbb{R}^m \to \mathbb{R}^n</math>. |
||
| + | |||
| + | When <math>C_v = 0</math>, we denote <math>C = C_p</math>. |
||
| + | |||
| + | By default <math>F = I</math>, <math>E = I</math>, <math>D = 0</math>, unless explicitly provided. |
||
| + | |||
| + | ===Other System Classes=== |
||
| + | Affine-parametric and time-varying versions of nonlinear systems are clearly also possible by combining patterns of the above models. |
||
Latest revision as of 15:28, 25 March 2024
Benchmark Model Templates
This page specifies templates for the types of models used as benchmark systems. In particular, the naming schemes established here are used in the corresponding data sets for all benchmarks. For example,  always serves as the name of the component matrix applied to the state
always serves as the name of the component matrix applied to the state 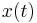 in a linear time-invariant, first-order system.
For all models we assume an input
in a linear time-invariant, first-order system.
For all models we assume an input 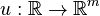 , with components
, with components 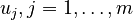 ,
a state
,
a state 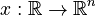 ,
and an output
,
and an output 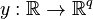 .
For all parametric models, we assume each component has
.
For all parametric models, we assume each component has  parameters; in cases where a component has fewer than
parameters; in cases where a component has fewer than  parameters, the extras are treated as
parameters, the extras are treated as 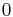 .
Some benchmarks (e.g., Bone Model) have a constant forcing term, in which case, it is assumed that
.
Some benchmarks (e.g., Bone Model) have a constant forcing term, in which case, it is assumed that  is identically
is identically 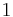 .
.
Linear Time-Invariant First-Order System (LTI-FOS)
with
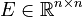 ,
,
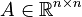 ,
,
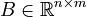 ,
,
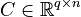 ,
,
 .
.
By default 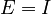 and
and 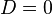 , unless explicitly provided.
, unless explicitly provided.
Linear Time-Varying First-Order System (LTV-FOS)
with
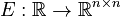 ,
,
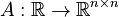 ,
,
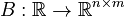 ,
,
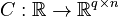 ,
,
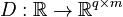 .
.
By default 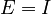 and
and 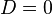 , unless explicitly provided.
, unless explicitly provided.
Affine-Parametric LTI-FOS (AP-LTI-FOS)
with
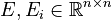 ;
;
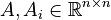 ;
;
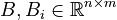 ; and
; and
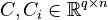 ,
for all
,
for all 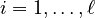 .
.
By default 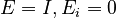 , unless explicitly provided. If
, unless explicitly provided. If  are provided without
are provided without  , then it is assumed
, then it is assumed 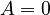 . Likewise for
. Likewise for  ,
,  , and
, and  .
.
Linear Time-Invariant Second-Order System (LTI-SOS)
with
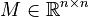 ,
,
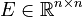 ,
,
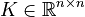 ,
,
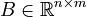 ,
,
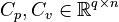 ,
,
 .
.
When 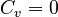 , we denote
, we denote 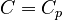 . By default
. By default 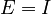 and
and 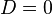 , unless explicitly provided.
, unless explicitly provided.
Affine-Parametric LTI-SOS (AP-LTI-SOS)
with
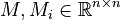 ;
;
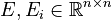 ;
;
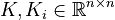 ;
;
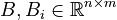 ; and
; and
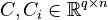 ,
for all
,
for all 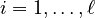 .
.
By default 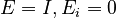 , unless explicitly provided. If
, unless explicitly provided. If 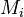 are provided without
are provided without  , then it is assumed
, then it is assumed 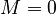 . Likewise for
. Likewise for 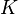 ,
,  , and
, and  .
.
Quadratic-Bilinear System (QBS)
with
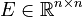 ,
,
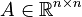 ,
,
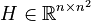 ,
,
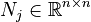 ,
,
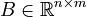 ,
,
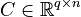 ,
,
 .
.
Nonlinear Time-Invariant First-Order System (NLTI-FOS)
with
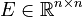 ,
,
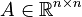 ,
,
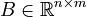 ,
,
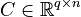 ,
,
 ,
,
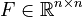 ,
,
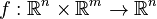 .
.
By default 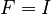 ,
, 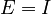 ,
, 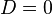 , unless explicitly provided.
, unless explicitly provided.
Nonlinear Time-Invariant Second-Order System (NLTI-SOS)
with
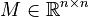 ,
,
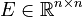 ,
,
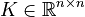 ,
,
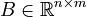 ,
,
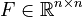 ,
,
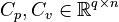 ,
,
 ,
,
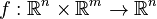 .
.
When 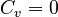 , we denote
, we denote 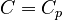 .
.
By default 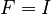 ,
, 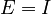 ,
, 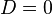 , unless explicitly provided.
, unless explicitly provided.
Other System Classes
Affine-parametric and time-varying versions of nonlinear systems are clearly also possible by combining patterns of the above models.