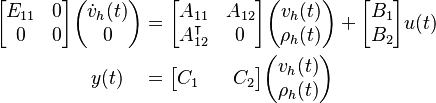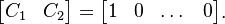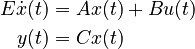(init Stokes) |
|||
| (4 intermediate revisions by one other user not shown) | |||
| Line 1: | Line 1: | ||
{{preliminary}} <!-- Do not remove --> |
{{preliminary}} <!-- Do not remove --> |
||
| + | [[Category:benchmark]] |
||
| + | [[Category:procedural]] |
||
| + | [[Category:SISO]] |
||
[[Category:linear]] |
[[Category:linear]] |
||
| + | [[Category:Sparse]] |
||
==Description== |
==Description== |
||
| + | This benchmark presents the two-dimensional instationary [[wikipedia:Stokes_flow|Stokes equation]], |
||
| + | which models flow of an incompressible fluid in a domain <ref name="Sty03"/>,<ref name="Sty04"/>,<ref name="MehS05"/>,<ref name="Sty06"/>,<ref name="Sch07"/>. |
||
| + | The associated partial differential equation system is given by: |
||
| + | :<math> |
||
| + | \begin{align} |
||
| + | \frac{\partial v}{\partial t} &= \Delta v - \nabla p + f, \qquad (x,t) \in \Omega \times (0,T] \\ |
||
| + | 0 &= \operatorname{div} v, \\ |
||
| + | v &= 0, \qquad \qquad \qquad \quad \; (x,t) \in \partial \Omega \times (0,T] |
||
| + | \end{align} |
||
| + | </math> |
||
| + | with velocity variable <math>v(x,t)</math> and pressure variable <math>\rho(x,t)</math>, |
||
| + | on a spatial domain <math>\Omega = [0,1] \times [0,1] \subset \mathbb{R}^2</math>, |
||
| + | and an external forcing term <math>f</math>. |
||
| + | The boundary conditions are no-slip. |
||
| + | A finite volume discretization on a uniform, staggered grid yields the descriptor system: |
||
| + | :<math> |
||
| + | \begin{align} |
||
| + | \begin{bmatrix} E_{11} & 0 \\ 0 & 0 \end{bmatrix} \begin{pmatrix} \dot{v}_h(t) \\ 0 \end{pmatrix} &= |
||
| + | \begin{bmatrix} A_{11} & A_{12} \\ A_{12}^\intercal & 0 \end{bmatrix} \begin{pmatrix} v_h(t) \\ \rho_h(t) \end{pmatrix} + |
||
| + | \begin{bmatrix} B_1 \\ B_2 \end{bmatrix} u(t) \\ |
||
| + | y(t)\quad & = \begin{bmatrix} C_1 \,\;&\;\, C_2 \end{bmatrix} \begin{pmatrix} v_h(t) \\ \rho_h(t) \end{pmatrix} |
||
| + | \end{align} |
||
| + | </math> |
||
| + | The matrix <math>A_{11}</math> matrix is the discretized Laplace operator, |
||
| + | while <math>A_{12}</math> corresponds to the discrete gradient and divergence operators. |
||
| + | For this benchmark the compound discretization of the boundary values and external forcing <math>[B_1 \; B_2]^\intercal \in \mathbb{R}^{N \times 1}</math> is chosen (uniformly) randomly, |
||
| + | whereas the output matrix <math>[C_1 \; C_2] \in \mathbb{R}^{1 \times N}</math> is set to: |
||
| + | :<math> |
||
| + | \begin{align} |
||
| + | \begin{bmatrix} C_1 & C_2 \end{bmatrix} = \begin{bmatrix} 1 & 0 & \dots & 0 \end{bmatrix}. |
||
| + | \end{align} |
||
| + | </math> |
||
| ⚫ | |||
| + | This is a procedural benchmark. |
||
| − | ==Origin== |
||
| + | A MATLAB m-file to generate <math>E, A, B, C</math> matrices can be found as part of the [https://www.mpi-magdeburg.mpg.de/projects/mess M.E.S.S] project, |
||
| + | under: |
||
| + | DEMOS/models/stokes/stokes_ind2.m |
||
| ⚫ | |||
| + | System structure: |
||
| ⚫ | |||
| + | :<math> |
||
| + | \begin{align} |
||
| + | E \dot{x}(t) &= Ax(t) + Bu(t) \\ |
||
| + | y(t) &= Cx(t) |
||
| + | \end{align} |
||
| + | </math> |
||
| + | System dimensions: |
||
| + | <math>E \in \mathbb{R}^{N \times N}</math>, |
||
| ⚫ | |||
| + | <math>A \in \mathbb{R}^{N \times N}</math>, |
||
| + | <math>B \in \mathbb{R}^{N \times 1}</math>, |
||
| + | <math>C \in \mathbb{R}^{1 \times N}</math>. |
||
| ⚫ | |||
| + | To cite this benchmark, use the following references: |
||
| + | * For the benchmark itself and its data: |
||
| ⚫ | |||
| + | ::The MORwiki Community, '''Stokes equation'''. MORwiki - Model Order Reduction Wiki, 2018. https://modelreduction.org/morwiki/Stokes_equation |
||
| + | @MISC{morwiki_stokes, |
||
| + | author = <nowiki>{{The MORwiki Community}}</nowiki>, |
||
| + | title = {Stokes equation}, |
||
| + | howpublished = {{MORwiki} -- Model Order Reduction Wiki}, |
||
| + | url = <nowiki>{https://modelreduction.org/morwiki/Stokes_equation}</nowiki>, |
||
| + | year = {20XX} |
||
| + | } |
||
| + | * For the background on the benchmark: |
||
| + | |||
| + | @PHDTHESIS{Sch07, |
||
| + | author = <nowiki>{M.Schmidt}</nowiki>, |
||
| + | title = {Systematic discretization of input/output maps and other contributions to the control of distributed parameter systems}, |
||
| + | school = {TU Berlin}, |
||
| + | year = {2007}, |
||
| + | doi = {10.14279/depositonce-1600} |
||
| + | } |
||
==References== |
==References== |
||
| + | <references> |
||
| + | |||
| + | <ref name="Sty03">T. Stykel. <span class="plainlinks">[https://doi.org/10.1002/pamm.200310302 Balanced truncation model reduction for descriptor systems]</span>, Proceedings in Applied Mathematics and Mechanics 3: 5--8, 2003.</ref> |
||
| + | |||
| + | <ref name="Sty04">T. Stykel. <span class="plainlinks">[https://doi.org/10.1007/s00498-004-0141-4 Gramian-Based Model Reduction for Descriptor System]</span>, Mathematics of Control, Signals, and Systems 16(4): 297--319, 2004.</ref> |
||
| + | |||
| + | <ref name="MehS05">V. Mehrmann, T. Stykel. <span class="plainlinks">[https://doi.org/10.1007/3-540-27909-1_3 Balanced Truncation Model Reduction for Large-Scale Systems in Descriptor Form]</span>, Dimension Reduction of Large-Scale Systems, Lecture Notes in Computational Science and Engineering, vol 45: 83--115, 2005.</ref> |
||
| + | |||
| + | <ref name="Sty06">T. Stykel. <span class="plainlinks">[https://doi.org/10.1016/j.laa.2004.01.015 Balanced Truncation model reduction for semidiscretized Stokes equation]</span>, Linear Algebra and its Application 415(2--3): 262--289, 2006.</ref> |
||
| + | |||
| + | <ref name="Sch07">M.Schmidt. <span class="plainlinks">[https://doi.org/10.14279/depositonce-1600 Systematic discretization of input/output maps and other contributions to the control of distributed parameter systems]</span>, Ph.D. thesis, TU Berlin, 2007.</ref> |
||
| + | |||
| + | </references> |
||
==Contact== |
==Contact== |
||
Latest revision as of 06:39, 17 June 2025
 Note: This page has not been verified by our editors.
Note: This page has not been verified by our editors.
Description
This benchmark presents the two-dimensional instationary Stokes equation, which models flow of an incompressible fluid in a domain [1],[2],[3],[4],[5]. The associated partial differential equation system is given by:
with velocity variable 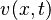 and pressure variable
and pressure variable 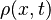 ,
on a spatial domain
,
on a spatial domain ![\Omega = [0,1] \times [0,1] \subset \mathbb{R}^2](/morwiki/images/math/5/2/a/52a66b1b7e6a3db2aef33f4c13f8c98a.png) ,
and an external forcing term
,
and an external forcing term 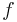 .
The boundary conditions are no-slip.
.
The boundary conditions are no-slip.
A finite volume discretization on a uniform, staggered grid yields the descriptor system:
The matrix 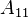 matrix is the discretized Laplace operator,
while
matrix is the discretized Laplace operator,
while 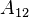 corresponds to the discrete gradient and divergence operators.
For this benchmark the compound discretization of the boundary values and external forcing
corresponds to the discrete gradient and divergence operators.
For this benchmark the compound discretization of the boundary values and external forcing ![[B_1 \; B_2]^\intercal \in \mathbb{R}^{N \times 1}](/morwiki/images/math/a/7/4/a74f83a828f5633b306d840d266ff230.png) is chosen (uniformly) randomly,
whereas the output matrix
is chosen (uniformly) randomly,
whereas the output matrix ![[C_1 \; C_2] \in \mathbb{R}^{1 \times N}](/morwiki/images/math/4/1/9/419c80fae8155eae9c868bef71fdbe5b.png) is set to:
is set to:
Data
This is a procedural benchmark.
A MATLAB m-file to generate 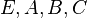 matrices can be found as part of the M.E.S.S project,
under:
matrices can be found as part of the M.E.S.S project,
under:
DEMOS/models/stokes/stokes_ind2.m
Dimensions
System structure:
System dimensions:
 ,
,
 ,
,
 ,
,
 .
.
Citation
To cite this benchmark, use the following references:
- For the benchmark itself and its data:
- The MORwiki Community, Stokes equation. MORwiki - Model Order Reduction Wiki, 2018. https://modelreduction.org/morwiki/Stokes_equation
@MISC{morwiki_stokes,
author = {{The MORwiki Community}},
title = {Stokes equation},
howpublished = {{MORwiki} -- Model Order Reduction Wiki},
url = {https://modelreduction.org/morwiki/Stokes_equation},
year = {20XX}
}
- For the background on the benchmark:
@PHDTHESIS{Sch07,
author = {M.Schmidt},
title = {Systematic discretization of input/output maps and other contributions to the control of distributed parameter systems},
school = {TU Berlin},
year = {2007},
doi = {10.14279/depositonce-1600}
}
References
- ↑ T. Stykel. Balanced truncation model reduction for descriptor systems, Proceedings in Applied Mathematics and Mechanics 3: 5--8, 2003.
- ↑ T. Stykel. Gramian-Based Model Reduction for Descriptor System, Mathematics of Control, Signals, and Systems 16(4): 297--319, 2004.
- ↑ V. Mehrmann, T. Stykel. Balanced Truncation Model Reduction for Large-Scale Systems in Descriptor Form, Dimension Reduction of Large-Scale Systems, Lecture Notes in Computational Science and Engineering, vol 45: 83--115, 2005.
- ↑ T. Stykel. Balanced Truncation model reduction for semidiscretized Stokes equation, Linear Algebra and its Application 415(2--3): 262--289, 2006.
- ↑ M.Schmidt. Systematic discretization of input/output maps and other contributions to the control of distributed parameter systems, Ph.D. thesis, TU Berlin, 2007.

![\begin{align}
\frac{\partial v}{\partial t} &= \Delta v - \nabla p + f, \qquad (x,t) \in \Omega \times (0,T] \\
0 &= \operatorname{div} v, \\
v &= 0, \qquad \qquad \qquad \quad \; (x,t) \in \partial \Omega \times (0,T]
\end{align}](/morwiki/images/math/0/f/2/0f27e911ee5f720dc7a92df241bc09ed.png)