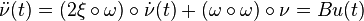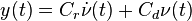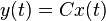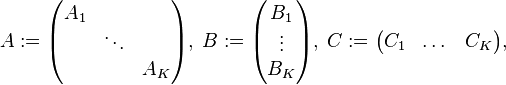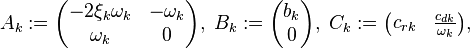(Init FSS Benchmark) |
|||
| (9 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{preliminary}} <!-- Do not remove --> |
||
| − | |||
[[Category:benchmark]] |
[[Category:benchmark]] |
||
[[Category:linear]] |
[[Category:linear]] |
||
[[Category:second differential order]] |
[[Category:second differential order]] |
||
| + | [[Category:Procedural]] |
||
[[Category:SISO]] |
[[Category:SISO]] |
||
==Description== |
==Description== |
||
| − | The '''flexible space structure''' benchmark<ref |
+ | The '''flexible space structure''' benchmark <ref name="gawronski90"/>,<ref name="gawronski91"/>,<ref name="gawronski96"/> is a procedural modal model which represents structural dynamics with a selectable number actuators and sensors. This model is used for truss structures in space environments i.e. the COFS-1 (Control of Flexible Structures) mast flight experiment <ref name="horner86"/>,<ref name="horta86"/>. |
| − | ==Model== |
+ | ===Model=== |
In modal form the '''flexible space structure''' model for <math>K</math> modes, <math>M</math> actuators and <math>Q</math> sensors is of second order and given by: |
In modal form the '''flexible space structure''' model for <math>K</math> modes, <math>M</math> actuators and <math>Q</math> sensors is of second order and given by: |
||
| + | |||
| ⚫ | |||
| − | \ddot{\nu}(t) |
+ | :<math>\ddot{\nu}(t) = (2 \xi \circ \omega) \circ \dot{\nu}(t) + (\omega \circ \omega) \circ \nu = Bu(t)</math> |
| + | |||
| − | + | :<math>y(t) = C_r\dot{\nu}(t) + C_d\nu(t)</math> |
|
| ⚫ | |||
| + | |||
| − | with the parameters <math>\xi \in \mathbb{R}_{>0}^K</math> (damping ratio), <math>\omega \in \mathbb{R}_{>0}^K</math> (natural frequency) and using the Hadamard product |
+ | with the parameters <math>\xi \in \mathbb{R}_{>0}^K</math> (damping ratio), <math>\omega \in \mathbb{R}_{>0}^K</math> (natural frequency) and using the Hadamard product <math>\circ</math>. |
| − | The first order representation follows for <math>x(t) = (\dot{nu}(t), \omega_1\nu_1, \dots, \omega_K\nu_K)</math> by: |
+ | The first order representation follows for <math>x(t) = (\dot{\nu}(t), \omega_1\nu_1, \dots, \omega_K\nu_K)</math> by: |
| − | :<math> |
||
| + | |||
| ⚫ | |||
| − | + | :<math>\dot{x}(t) = Ax(t) + Bu(t) </math> |
|
| + | |||
| − | </math> |
||
| + | :<math>y(t) = Cx(t)</math> |
||
| + | |||
with the matrices: |
with the matrices: |
||
| + | |||
| − | :<math> |
||
| − | A := \begin{pmatrix} A_1 & & \\ & \ddots & \\ & & A_K \end{pmatrix}, \\ |
+ | :<math>A := \begin{pmatrix} A_1 & & \\ & \ddots & \\ & & A_K \end{pmatrix}, \; B := \begin{pmatrix} B_1 \\ \vdots \\ B_K \end{pmatrix}, \; C := \begin{pmatrix} C_1 & \dots & C_K \end{pmatrix}, </math> |
| + | |||
| − | B := \begin{pmatrix} B_1 \\ \vdots \\ B_K \end{pmatrix}, \\ |
||
| − | C := \begin{pmatrix} C_1 & \dots & C_K \end{pmatrix}, |
||
| − | </math> |
||
and their components: |
and their components: |
||
| + | |||
| − | :<math> |
||
| − | A_k := \begin{pmatrix} -2\xi_k\omega_k & -\omega_k \\ \omega_k & 0 \end{pmatrix}, \\ |
+ | :<math>A_k := \begin{pmatrix} -2\xi_k\omega_k & -\omega_k \\ \omega_k & 0 \end{pmatrix}, \; B_k := \begin{pmatrix} b_k \\ 0 \end{pmatrix}, \; C_k := \begin{pmatrix} c_{rk} & \frac{c_{dk}}{\omega_k} \end{pmatrix},</math> |
| + | |||
| − | B_k := \begin{pmatrix} b_k \\ 0 \end{pmatrix}, \\ |
||
| − | C_k := \begin{pmatrix} c_{rk} & \frac{c_{dk}}{\omega_k} \end{pmatrix}, |
||
| − | </math> |
||
where <math>b_k \in \mathbb{R}^{1 \times M}</math> and <math>c_{rk}, c_{dk} \in \mathbb{R}^{Q \times 1}</math>. |
where <math>b_k \in \mathbb{R}^{1 \times M}</math> and <math>c_{rk}, c_{dk} \in \mathbb{R}^{Q \times 1}</math>. |
||
| Line 41: | Line 38: | ||
For this benchmark the system matrix is block diagonal and thus chosen to be sparse. |
For this benchmark the system matrix is block diagonal and thus chosen to be sparse. |
||
| − | The parameters <math>\xi</math> and math>\omega</math> are sampled from a uniform random distributions <math>\mathcal{U}_[0,\frac{1}{1000}]}^K</math> and <math>\mathcal{U}_[0,100]}^K</math> respectively. |
+ | The parameters <math>\xi</math> and <math>\omega</math> are sampled from a uniform random distributions <math>\mathcal{U}_{[0,\frac{1}{1000}]}^K</math> and <math>\mathcal{U}_{[0,100]}^K</math> respectively. |
The components of the input matrix <math>b_k</math> are sampled form a uniform random distribution <math>\mathcal{U}_{[0,1]}</math>, |
The components of the input matrix <math>b_k</math> are sampled form a uniform random distribution <math>\mathcal{U}_{[0,1]}</math>, |
||
| − | while the output matrix <math>C</math> is sampled from a uniform random distribution <math>\mathcal{U |
+ | while the output matrix <math>C</math> is sampled from a uniform random distribution <math>\mathcal{U}_{[0,10]}</math> completely w.l.o.g, since if the components of <math>C_d</math> are random their scaling can be ignored. |
==Data== |
==Data== |
||
| − | The following Matlab code assembles the above described <math>A</math>, <math>B</math> and <math>C</math> matrix for a given number of modes <math>K</math>. |
+ | The following Matlab code assembles the above described <math>A</math>, <math>B</math> and <math>C</math> matrix for a given number of modes <math>K</math>, actuators (inputs) <math>M</math> and sensors (outputs) <math>Q</math>. |
<div class="thumbinner" style="width:540px;text-align:left;"> |
<div class="thumbinner" style="width:540px;text-align:left;"> |
||
| Line 56: | Line 53: | ||
rand('seed',1009); |
rand('seed',1009); |
||
xi = rand(1,K)*0.001; % Sample damping ratio |
xi = rand(1,K)*0.001; % Sample damping ratio |
||
| − | omega = rand(1,K)*100; % Sample natural frequencies |
+ | omega = rand(1,K)*100.0; % Sample natural frequencies |
A_k = cellfun(@(p) sparse([-2.0*p(1)*p(2),-p(2);p(2),0]), ... |
A_k = cellfun(@(p) sparse([-2.0*p(1)*p(2),-p(2);p(2),0]), ... |
||
| Line 70: | Line 67: | ||
</div> |
</div> |
||
| + | ==Dimensions== |
||
| + | |||
| + | System structure: |
||
| ⚫ | |||
| + | \begin{align} |
||
| ⚫ | |||
| + | y(t) &= Cx(t) |
||
| + | \end{align} |
||
| ⚫ | |||
| + | |||
| + | System dimensions: |
||
| + | |||
| + | <math>A \in \mathbb{R}^{2K \times 2K}</math>, |
||
| + | <math>B \in \mathbb{R}^{2K \times M}</math>, |
||
| + | <math>C \in \mathbb{R}^{Q \times 2K}</math>. |
||
| + | |||
| + | ==Citation== |
||
| + | |||
| + | To cite this benchmark, use the following references: |
||
| + | |||
| + | * For the benchmark itself and its data: |
||
| + | ::The MORwiki Community, '''Flexible Space Structures'''. MORwiki - Model Order Reduction Wiki, 2018. http://modelreduction.org/index.php/Flexible_Space_Structures |
||
| + | |||
| + | @MISC{morwiki-flexspacstruc, |
||
| + | author = <nowiki>{{The MORwiki Community}}</nowiki>, |
||
| + | title = {Flexible Space Structures}, |
||
| + | howpublished = {{MORwiki} -- Model Order Reduction Wiki}, |
||
| + | url = <nowiki>{https://modelreduction.org/morwiki/Flexible_Space_Structures}</nowiki>, |
||
| + | year = 2018 |
||
| + | } |
||
| + | |||
| + | * For the background on the benchmark: [https://morwiki.mpi-magdeburg.mpg.de/BibTeX/#morGawW91 morGawW91] ([https://morwiki.mpi-magdeburg.mpg.de/BibTeX/html/mor_bib.html#morGawW91 BibTeX]) |
||
==Reference== |
==Reference== |
||
| − | <references |
+ | <references> |
| + | |||
| + | <ref name="gawronski90">W. Gawronski and J.N. Juang. "<span class="plainlinks">[https://doi.org/10.1016/B978-0-12-012736-8.50010-3 Model Reduction for Flexible Structures]</span>", Control and Dynamic Systems, 36: 143--222, 1990.</ref> |
||
| + | |||
| + | <ref name="gawronski91">W. Gawronski and T. Williams, "<span class="plainlinks">[http://doi.org/10.2514/3.20606 Model Reduction for Flexible Space Structures]</span>", Journal of Guidance 14(1): 68--76, 1991</ref> |
||
| + | |||
| + | <ref name="gawronski96">W. Gawronski. "<span class="plainlinks">[https://doi.org/10.1007/3540760172_4 Model reduction]</span>". In: Balanced Control of Flexible Structures. Lecture Notes in Control and Information Sciences, vol 211: 45--106, 1996.</ref> |
||
| + | |||
| + | <ref name="horner86">G.C. Horner. "<span class="plainlinks">[https://ntrs.nasa.gov/search.jsp?R=19870006596 COFS-1 Research Overview]</span>". NASA / DOD Control Structures Interaction Technology: 233--251, 1986</ref> |
||
| + | |||
| + | <ref name="horta86">L.G. Horta, J.L. Walsh, G.C. Horner and J.P. Bailey. "<span class="plainlinks">[https://ntrs.nasa.gov/search.jsp?R=19870006613 Analysis and simulation of the MAST (COFS-1 flight hardware)]</span>". NASA / DOD Control Structures Interaction Technology: 515--532, 1986.</ref> |
||
| + | |||
| + | </references> |
||
==Contact== |
==Contact== |
||
Latest revision as of 06:31, 17 June 2025
Description
The flexible space structure benchmark [1],[2],[3] is a procedural modal model which represents structural dynamics with a selectable number actuators and sensors. This model is used for truss structures in space environments i.e. the COFS-1 (Control of Flexible Structures) mast flight experiment [4],[5].
Model
In modal form the flexible space structure model for 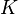 modes,
modes,  actuators and
actuators and  sensors is of second order and given by:
sensors is of second order and given by:
with the parameters 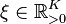 (damping ratio),
(damping ratio), 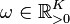 (natural frequency) and using the Hadamard product
(natural frequency) and using the Hadamard product  .
The first order representation follows for
.
The first order representation follows for 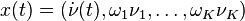 by:
by:
with the matrices:
and their components:
where 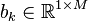 and
and 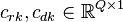 .
.
Benchmark Specifics
For this benchmark the system matrix is block diagonal and thus chosen to be sparse.
The parameters 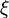 and
and  are sampled from a uniform random distributions
are sampled from a uniform random distributions ![\mathcal{U}_{[0,\frac{1}{1000}]}^K](/morwiki/images/math/2/4/b/24b74811b308c537765802cb07a302f7.png) and
and ![\mathcal{U}_{[0,100]}^K](/morwiki/images/math/3/4/2/342f256255fdd3d862d8d938a73b7d07.png) respectively.
The components of the input matrix
respectively.
The components of the input matrix 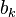 are sampled form a uniform random distribution
are sampled form a uniform random distribution ![\mathcal{U}_{[0,1]}](/morwiki/images/math/8/9/1/8914ff20760d02f585b13a7a84bf17e7.png) ,
while the output matrix
,
while the output matrix  is sampled from a uniform random distribution
is sampled from a uniform random distribution ![\mathcal{U}_{[0,10]}](/morwiki/images/math/9/e/7/9e7fb3f2b81367f97ff7a31de6e468bb.png) completely w.l.o.g, since if the components of
completely w.l.o.g, since if the components of 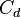 are random their scaling can be ignored.
are random their scaling can be ignored.
Data
The following Matlab code assembles the above described  ,
,  and
and  matrix for a given number of modes
matrix for a given number of modes 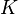 , actuators (inputs)
, actuators (inputs)  and sensors (outputs)
and sensors (outputs)  .
.
function [A,B,C] = fss(K,M,Q)
rand('seed',1009);
xi = rand(1,K)*0.001; % Sample damping ratio
omega = rand(1,K)*100.0; % Sample natural frequencies
A_k = cellfun(@(p) sparse([-2.0*p(1)*p(2),-p(2);p(2),0]), ...
num2cell([xi;omega],1),'UniformOutput',0);
A = blkdiag(A_k{:});
B = kron(rand(K,M),[1;0]);
C = 10.0*rand(Q,2*K);
end
Dimensions
System structure:
System dimensions:
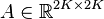 ,
,
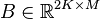 ,
,
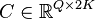 .
.
Citation
To cite this benchmark, use the following references:
- For the benchmark itself and its data:
- The MORwiki Community, Flexible Space Structures. MORwiki - Model Order Reduction Wiki, 2018. http://modelreduction.org/index.php/Flexible_Space_Structures
@MISC{morwiki-flexspacstruc,
author = {{The MORwiki Community}},
title = {Flexible Space Structures},
howpublished = {{MORwiki} -- Model Order Reduction Wiki},
url = {https://modelreduction.org/morwiki/Flexible_Space_Structures},
year = 2018
}
Reference
- ↑ W. Gawronski and J.N. Juang. "Model Reduction for Flexible Structures", Control and Dynamic Systems, 36: 143--222, 1990.
- ↑ W. Gawronski and T. Williams, "Model Reduction for Flexible Space Structures", Journal of Guidance 14(1): 68--76, 1991
- ↑ W. Gawronski. "Model reduction". In: Balanced Control of Flexible Structures. Lecture Notes in Control and Information Sciences, vol 211: 45--106, 1996.
- ↑ G.C. Horner. "COFS-1 Research Overview". NASA / DOD Control Structures Interaction Technology: 233--251, 1986
- ↑ L.G. Horta, J.L. Walsh, G.C. Horner and J.P. Bailey. "Analysis and simulation of the MAST (COFS-1 flight hardware)". NASA / DOD Control Structures Interaction Technology: 515--532, 1986.