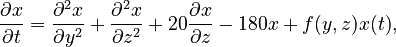(init pde) |
m (infobox string) |
||
| (7 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{preliminary}} <!-- Do not remove --> |
||
| − | |||
[[Category:benchmark]] |
[[Category:benchmark]] |
||
[[Category:SLICOT]] |
[[Category:SLICOT]] |
||
| + | [[Category:linear]] |
||
| + | [[Category:time invariant]] |
||
| + | [[Category:first differential order]] |
||
[[Category:Sparse]] |
[[Category:Sparse]] |
||
[[Category:SISO]] |
[[Category:SISO]] |
||
| + | {{Infobox |
||
| − | '''This is a stub. Please expand.''' |
||
| + | |Title = Convection Reaction |
||
| + | |Benchmark ID = convectionReaction_n84m1q1 |
||
| + | |Category = slicot |
||
| + | |System-Class = LTI-FOS |
||
| + | |nstates = 84 |
||
| + | |ninputs = 1 |
||
| + | |noutputs = 1 |
||
| + | |nparameters = 0 |
||
| + | |components = A, B, C |
||
| + | |License = NA |
||
| + | |Creator = [[User:Himpe]] |
||
| + | |Editor = |
||
| + | * [[User:Himpe]] |
||
| + | * [[User:Mlinaric]] |
||
| + | |Zenodo-link = NA |
||
| + | }} |
||
==Description== |
==Description== |
||
| − | This benchmark models a chemical reaction by a [[wikipedia:Convection-diffusion_equation|convection]]-[[wikipedia:Reaction-diffusion|reaction]] partial differential equation |
+ | This benchmark models a chemical reaction by a [[wikipedia:Convection-diffusion_equation|convection]]-[[wikipedia:Reaction-diffusion|reaction]] partial differential equation on the unit square, |
| + | given by: |
||
| ⚫ | |||
| + | :<math> |
||
| + | \frac{\partial x}{\partial t} = \frac{\partial^2 x}{\partial y^2} + \frac{\partial^2 x}{\partial z^2} + 20 \frac{\partial x}{\partial z} - 180 x + f(y,z) x(t), |
||
| + | </math> |
||
| + | |||
| + | with Dirichlet boundary conditions and discretized with centered difference approximation. |
||
| + | |||
| + | The input vector <math>B</math> is composed of random elements and the output vector equals the input vector <math>C = B^T</math>. |
||
| + | |||
| ⚫ | |||
==Origin== |
==Origin== |
||
This benchmark is part of the '''SLICOT Benchmark Examples for Model Reduction'''<ref name="chahlaoui05"/>. |
This benchmark is part of the '''SLICOT Benchmark Examples for Model Reduction'''<ref name="chahlaoui05"/>. |
||
| − | |||
==Data== |
==Data== |
||
| − | The system matrices <math>A</math>, <math>B</math>, <math>C</math> are available from the [ |
+ | The system matrices <math>A</math>, <math>B</math>, <math>C</math> are available from the [https://www.slicot.org/20-site/126-benchmark-examples-for-model-reduction SLICOT benchmarks] page: [https://www.slicot.org/objects/software/shared/bench-data/pde.zip pde.zip] and are stored as MATLAB [https://www.mathworks.com/help/matlab/import_export/mat-file-versions.html .mat] file. |
| + | Here is [https://www.python.org Python] code for loading the matrices (<math>A</math> is a sparse matrix of 16-bit integers and <math>B</math> and <math>C</math> are full matrices stored as sparse matrices): |
||
| + | |||
| + | :<syntaxhighlight lang="python"> |
||
| + | import numpy as np |
||
| + | from scipy.io import loadmat |
||
| + | |||
| + | mat = loadmat('build.mat') |
||
| + | A = mat['A'].astype(np.float64) |
||
| + | B = mat['B'].toarray() |
||
| + | C = mat['C'].toarray() |
||
| + | </syntaxhighlight> |
||
==Dimensions== |
==Dimensions== |
||
| Line 29: | Line 65: | ||
:<math> |
:<math> |
||
| − | \begin{ |
+ | \begin{align} |
| − | \dot{x}(t) &= |
+ | \dot{x}(t) &= A x(t) + B u(t) \\ |
| − | y(t) &= |
+ | y(t) &= C x(t) |
| − | \end{ |
+ | \end{align} |
</math> |
</math> |
||
| Line 40: | Line 76: | ||
<math>B \in \mathbb{R}^{84 \times 1}</math>, |
<math>B \in \mathbb{R}^{84 \times 1}</math>, |
||
<math>C \in \mathbb{R}^{1 \times 84}</math>. |
<math>C \in \mathbb{R}^{1 \times 84}</math>. |
||
| − | |||
==Citation== |
==Citation== |
||
| Line 77: | Line 112: | ||
<ref name="saad88"> Y. Saad. <span class="plainlinks">[https://doi.org/10.1109/9.406 Projection and deflation method for partial pole assignment in linear state feedback]</span>, IEEE Transactions on Automatic Control, 33(3): 290--297, 1988.</ref> |
<ref name="saad88"> Y. Saad. <span class="plainlinks">[https://doi.org/10.1109/9.406 Projection and deflation method for partial pole assignment in linear state feedback]</span>, IEEE Transactions on Automatic Control, 33(3): 290--297, 1988.</ref> |
||
| − | <ref name="grimme97"> E.J. Grimme. <span class="plainlinks">[ |
+ | <ref name="grimme97"> E.J. Grimme. <span class="plainlinks">[https://www.proquest.com/dissertations-theses/krylov-projection-methods-model-reduction/docview/304361372/se-2?accountid=14597 Krylov Projection Methods for Model Reduction]</span>. PhD Thesis, University of Illinois at Urbana-Champaign, 1998.</ref> |
<ref name="chahlaoui02"> Y. Chahlaoui, P. Van Dooren, <span class="plainlinks">[http://eprints.maths.manchester.ac.uk/1040/1/ChahlaouiV02a.pdf A collection of Benchmark examples for model reduction of linear time invariant dynamical systems]</span>, Working Note 2002-2: 2002.</ref> |
<ref name="chahlaoui02"> Y. Chahlaoui, P. Van Dooren, <span class="plainlinks">[http://eprints.maths.manchester.ac.uk/1040/1/ChahlaouiV02a.pdf A collection of Benchmark examples for model reduction of linear time invariant dynamical systems]</span>, Working Note 2002-2: 2002.</ref> |
||
Latest revision as of 10:28, 30 November 2023
| Background | |
|---|---|
| Benchmark ID |
convectionReaction_n84m1q1 |
| Category |
slicot |
| System-Class |
LTI-FOS |
| Parameters | |
| nstates |
84
|
| ninputs |
1 |
| noutputs |
1 |
| nparameters |
0 |
| components |
A, B, C |
| Copyright | |
| License |
NA |
| Creator | |
| Editor | |
| Location | |
|
NA | |
Description
This benchmark models a chemical reaction by a convection-reaction partial differential equation on the unit square, given by:
with Dirichlet boundary conditions and discretized with centered difference approximation.
The input vector  is composed of random elements and the output vector equals the input vector
is composed of random elements and the output vector equals the input vector 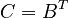 .
.
More details can be found in [1], [2], [3] and [4], [5].
Origin
This benchmark is part of the SLICOT Benchmark Examples for Model Reduction[5].
Data
The system matrices  ,
,  ,
,  are available from the SLICOT benchmarks page: pde.zip and are stored as MATLAB .mat file.
are available from the SLICOT benchmarks page: pde.zip and are stored as MATLAB .mat file.
Here is Python code for loading the matrices ( is a sparse matrix of 16-bit integers and
is a sparse matrix of 16-bit integers and  and
and  are full matrices stored as sparse matrices):
are full matrices stored as sparse matrices):
import numpy as np from scipy.io import loadmat mat = loadmat('build.mat') A = mat['A'].astype(np.float64) B = mat['B'].toarray() C = mat['C'].toarray()
Dimensions
System structure:
System dimensions:
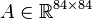 ,
,
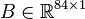 ,
,
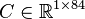 .
.
Citation
To cite this benchmark, use the following references:
- For the benchmark itself and its data:
- Niconet e.V., SLICOT - Subroutine Library in Systems and Control Theory, http://www.slicot.org
@MANUAL{slicot_pde,
title = {{SLICOT} - Subroutine Library in Systems and Control Theory},
organization = {Niconet e.V.},
address = {\url{http://www.slicot.org}},
key = {SLICOT}
}
- For the background on the benchmark:
@ARTICLE{Saa88,
author = {Y. Saad},
title = {Projection and deflation method for partial pole assignment in linear state feedback},
journal = {IEEE Transactions on Automatic Control},
volume = {33},
number = {3},
pages = {290--297},
year = {1988},
doi = {10.1109/9.406}
}
References
- ↑ P. Raschman, M. Kuhicek, M. Maros. Waves in distributed chemical systems: Experiments and computations. In: New Approaches to Nonlinear Problems in Dynamics - Proceedings of the Asilomar Conference Ground: 271--288, SIAM, 1980.
- ↑ Y. Saad. Projection and deflation method for partial pole assignment in linear state feedback, IEEE Transactions on Automatic Control, 33(3): 290--297, 1988.
- ↑ E.J. Grimme. Krylov Projection Methods for Model Reduction. PhD Thesis, University of Illinois at Urbana-Champaign, 1998.
- ↑ Y. Chahlaoui, P. Van Dooren, A collection of Benchmark examples for model reduction of linear time invariant dynamical systems, Working Note 2002-2: 2002.
- ↑ 5.0 5.1 Y. Chahlaoui, P. Van Dooren, Benchmark Examples for Model Reduction of Linear Time-Invariant Dynamical Systems, Dimension Reduction of Large-Scale Systems, Lecture Notes in Computational Science and Engineering, vol 45: 379--392, 2005.