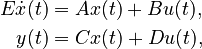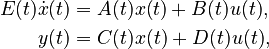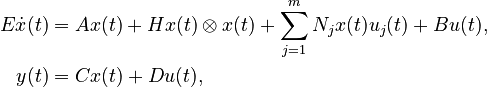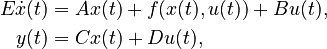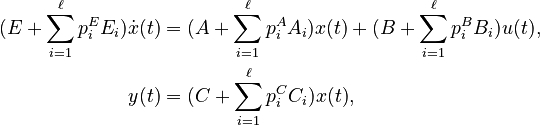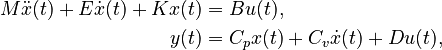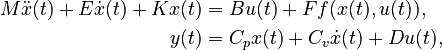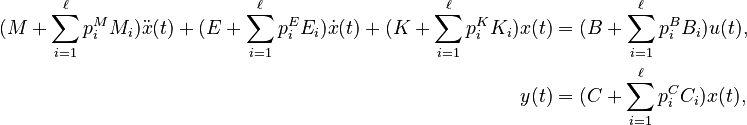m (→Quadratic-Bilinear System: add acronym) |
(→Nonlinear Time-Invariant System: expand section title) |
||
| Line 62: | Line 62: | ||
<math>D \in \mathbb{R}^{q \times m}</math>. |
<math>D \in \mathbb{R}^{q \times m}</math>. |
||
| − | ===Nonlinear Time-Invariant System=== |
+ | ===Nonlinear Time-Invariant First-Order System (NLTI-FOS)=== |
:<math> |
:<math> |
||
| Line 79: | Line 79: | ||
<math>D \in \mathbb{R}^{q \times m}</math>, |
<math>D \in \mathbb{R}^{q \times m}</math>, |
||
<math>f : \mathbb{R}^n \times \mathbb{R}^m \to \mathbb{R}^n</math>. |
<math>f : \mathbb{R}^n \times \mathbb{R}^m \to \mathbb{R}^n</math>. |
||
| − | |||
===Affine Parametric Linear Time-Invariant System=== |
===Affine Parametric Linear Time-Invariant System=== |
||
Revision as of 20:00, 20 April 2023
Benchmark Model Templates
This page specifies templates for the types of models used as benchmark systems. In particular, the naming schemes established here are used in the corresponding data sets for all benchmarks. For example,  always serves as the name of the component matrix applied to the state
always serves as the name of the component matrix applied to the state 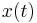 in a linear time-invariant system.
For all models we assume an input
in a linear time-invariant system.
For all models we assume an input 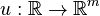 , with components
, with components 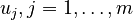 ,
a state
,
a state 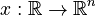 ,
and an output
,
and an output 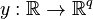 .
For all parametric models, we assume each component has
.
For all parametric models, we assume each component has  parameters; in cases where a component has fewer than
parameters; in cases where a component has fewer than  parameters, the extras are treated as
parameters, the extras are treated as 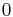 .
Some benchmarks (e.g., Bone Model) have a constant forcing term, in which case, it is assumed that
.
Some benchmarks (e.g., Bone Model) have a constant forcing term, in which case, it is assumed that  is identically
is identically 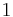 .
.
Linear Time-Invariant First-Order System (LTI-FOS)
with
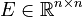 ,
,
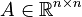 ,
,
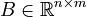 ,
,
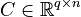 ,
,
 .
.
Linear Time-Varying First-Order System (LTV-FOS)
with
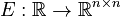 ,
,
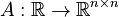 ,
,
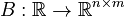 ,
,
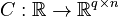 ,
,
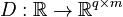 .
.
Quadratic-Bilinear System (QBS)
with
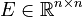 ,
,
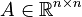 ,
,
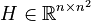 ,
,
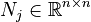 ,
,
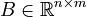 ,
,
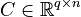 ,
,
 .
.
Nonlinear Time-Invariant First-Order System (NLTI-FOS)
with
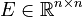 ,
,
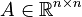 ,
,
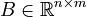 ,
,
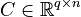 ,
,
 ,
,
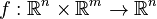 .
.
Affine Parametric Linear Time-Invariant System
with
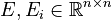 ;
;
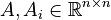 ;
;
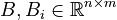 ; and
; and
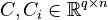 ,
for all
,
for all 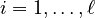 .
.
Second-Order System
with
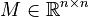 ,
,
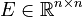 ,
,
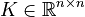 ,
,
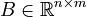 ,
,
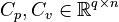 ,
,
 .
.
When 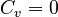 , we denote
, we denote 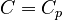 .
.
Nonlinear Second-Order System
with
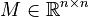 ,
,
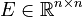 ,
,
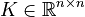 ,
,
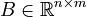 ,
,
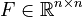 ,
,
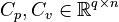 ,
,
 ,
,
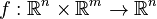 .
.
When 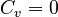 , we denote
, we denote 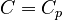 .
.
Affine Parametric Second-Order System
with
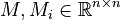 ;
;
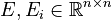 ;
;
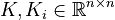 ;
;
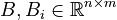 ; and
; and
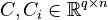 ,
for all
,
for all 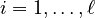 .
.