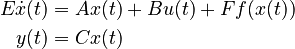| Background | |
|---|---|
| Benchmark ID |
|
| Category |
oberwolfach |
| System-Class |
|
| Parameters | |
| nstates |
|
| ninputs |
2 |
| noutputs |
2 |
| nparameters |
0 |
| components |
|
| Copyright | |
| License |
NA |
| Creator | |
| Editor | |
| Location | |
|
NA | |
Description
The simulation of heat transport for a single device is easily tackled by current computational resources, even for a complex, finely structured geometry; however, the calculation of a multi-scale system consisting of a large number of those devices, e.g., assembled printed circuit boards, is still a challenge. A further problem is the large change in heat conductivity of many semiconductor materials with temperature. We model the heat transfer along a 1D beam that has a nonlinear heat capacity which is represented by a polynomial of arbitrary degree as a function of the temperature state. For accurate modelling of the temperature distribution, the resulting model requires many state variables to be described adequately. The resulting complexity, i.e., number of first order differential equations and nonlinear parts, is such that a simplification or model reduction is needed in order to perform a simulation in an acceptable amount of time for the applications at hand. Thus the need for model order reduction emerges.
Model description
We model the heat transfer along a 1D beam with length 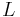 , cross sectional area
, cross sectional area  and nonlinear heat conductivity represented by a polynomial in temperature
and nonlinear heat conductivity represented by a polynomial in temperature 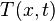 of arbitrary degree
of arbitrary degree  :
:
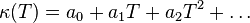
The output of the model is the temperature 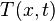 , the degrees of freedom are the temperature from left to right.
The right end of the beam (at
, the degrees of freedom are the temperature from left to right.
The right end of the beam (at 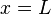 ) is fixed at ambient temperature
) is fixed at ambient temperature 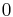 ;
this node does not occur in the model any more.
The model features two inputs: The first one is a time-dependent uniform heat flux
;
this node does not occur in the model any more.
The model features two inputs: The first one is a time-dependent uniform heat flux 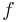 [W/m2] flowing in from the left end (at
[W/m2] flowing in from the left end (at 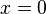 ).
The second one is a time dependent heat source
).
The second one is a time dependent heat source  [W/m3] in the beam volume, e.g. from an electric current.
[W/m3] in the beam volume, e.g. from an electric current.
Benchmark examples
An interactive matrix generator has been created using Wolfram Research's webMathematica. Models produced by this generator are in the DSIF format, which allows for nonlinear terms.
Three ready-made examples are available (all files are gzip compressed DSIF files, Units: SI):
Linear example (heat conductivity not temperature dependent)
| Property | Symbol | Unit | Value |
| Number of nodes | 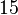
| ||
| Beam length | 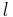
|
[m] | 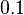
|
| Cross-sectional area | 
|
[m2] | 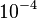
|
| Material density | 
|
[kg/m3] | 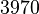
|
| Heat capacity | 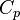
|
[J/kg K] | 
|
| Heat conductivity | 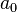
|
[W/m K] | 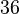
|
Nonlinear examples (heat conductivity temperature dependent)
| Property | Symbol | Unit | Value |
| Number of nodes | 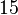
| ||
| Beam length | 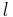
|
[m] | 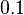
|
| Cross-sectional area | 
|
[m2] | 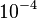
|
| Material density | 
|
[kg/m3] | 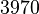
|
| Heat capacity | 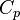
|
[J/kg K] | 
|
| Heat conductivity | 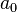
|
[W/m K] | 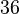
|
| Heat conductivity | 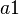
|
[W/m K2] | 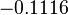
|
| Heat conductivity | 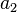
|
[W/m K3] | 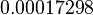
|
| Heat conductivity | 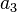
|
[W/m K4] | 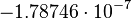
|
| Heat conductivity | 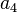
|
[W/m K5] | 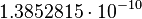
|
| Property | Symbol | Unit | Value |
| Number of nodes | 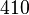
| ||
| Beam length | 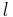
|
[m] | 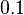
|
| Cross-sectional area | 
|
[m2] | 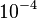
|
| Material density | 
|
[kg/m3] | 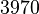
|
| Heat capacity | 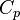
|
[J/kg K] | 
|
| Heat conductivity | 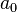
|
[W/m K] | 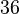
|
| Heat conductivity | 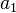
|
[W/m K2] | 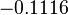
|
| Heat conductivity | 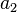
|
[W/m K3] | 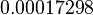
|
| Heat conductivity | 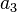
|
[W/m K4] | 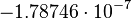
|
| Heat conductivity | 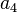
|
[W/m K5] | 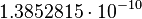
|
The .m files contain matrices  ,
,  ,
,  ,
,  and
and  and the vector
and the vector 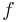 for the following system of equations:
for the following system of equations:
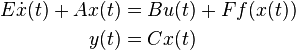
The two outputs are on the left end and in the middle of the beam.
Origin
This benchmark is part of the Oberwolfach Benchmark Collection[1]; No. 38883, see [2].
Data
Details of the implementation are available in a separate report[3]. A typical input to this system is a step response; periodic on/off switching is also possible. The reduced model should thus both represent the step response as well as the possible influence of higher order harmonics.
| NonlinearHeatTransfer-dim1e1-n15-linear.zip | 1 kB |
| NonlinearHeatTransfer-dim1e1-n15-nonlinear.zip | 1.2 kB |
| NonlinearHeatTransfer-dim1e2-n410-nonlinear.zip | 18.8 kB |
Dimensions
System structure:
System dimensions:
 ,
,
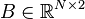 ,
,
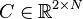 ,
,
 ,
,
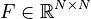 ,
,
 .
.
System variants:
n15-linear: 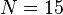 ,
n15-nonlinear:
,
n15-nonlinear: 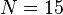 ,
n410-nonlinear:
,
n410-nonlinear: 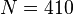 .
.
Citation
To cite this benchmark, use the following references:
- For the benchmark itself and its data:
- The MORwiki Community, Nonlinear Heat Transfer. MORwiki - Model Order Reduction Wiki, 2018. https://modelreduction.org/morwiki/Nonlinear_Heat_Transfer
@MISC{morwiki_nheat,
author = {{The MORwiki Community}},
title = {Nonlinear Heat Transfer},
howpublished = {{MORwiki} -- Model Order Reduction Wiki},
url = {https://modelreduction.org/morwiki/Nonlinear_Heat_Transfer},
year = {20XX}
}
- For the background on the benchmark:
@INPROCEEDINGS{LieYK04,
author = {J. Lienemann, A. Yousefi, J.G. Korvink},
title = {Nonlinear heat transfer modelling},
booktile = {12th Mediterranean Conference on Control and Automation},
year = {2004}
}
References
- ↑ J.G. Korvink, E.B. Rudnyi, Oberwolfach Benchmark Collection, In: Dimension Reduction of Large-Scale Systems, Lecture Notes in Computational Science and Engineering, vol 45: 311--315, 2005.
- ↑ J. Lienemann, A. Yousefi, J.G. Korvink, Nonlinear Heat Transfer Modeling, In: Dimension Reduction of Large-Scale Systems, Lecture Notes in Computational Science and Engineering, vol 45: 327--331, 2005.
- ↑ J. Lienemann, A. Yousefi, J.G. Korvink, Nonlinear heat transfer modelling, 12th Mediterranean Conference on Control and Automation, 2004.