Bilinear PMOR method

The model reduction method we present here is applicable to linear parameter-varying (LPV) systems of the form

$\dot{x}(t)=Ax(t) + \sum_{i=1}^d p_i(t)A_i x(t)+B_0u_0(t),\quad y(t)=Cx(t),$

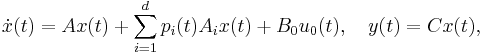
where 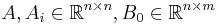$A,A_i \in \mathbb R^{n\times n}, B_0 \in \mathbb R^{n\times m}$ and $C \in \mathbb R^{p\times n}.$

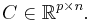
The main idea is that the structure of the above type of systems is quite similar to so-called bilinear control systems. Although belonging to the class of nonlinear control systems, the latter exhibit many features of linear time-invariant systems. In more detail, a bilinear control system is given as follows

$\dot{x}(t)=Ax(t) + \sum_{i=1}^m N_i x(t) u_i(t) + B u(t),$

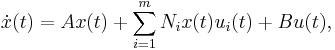
where 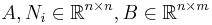$A,N_i \in \mathbb R^{n\times n}, B \in \mathbb R^{n\times m}$ and $C \in \mathbb R^{p\times n}.$

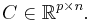
As one can see, there seems to be a close connection between LPV and bilinear systems which may be advantageous. To be more precise, following [2], we can interpret LPV systems as special bilinear system by simply setting

$\tilde{A}=A,\;\; \tilde{N}_i=0,\;\;i=1,\dots,m,\;\; \tilde{N}_i=A_i,\;\; i=m+1,\dots,m+d, \;\; \tilde{B}=\begin{bmatrix} B_0 & 0\end{bmatrix},\;\; \tilde{C}=C, \;\; \tilde{u}=\begin{bmatrix} u_0 \\ p_1(t) \\ \vdots \\ p_d(t)\end{bmatrix} .$

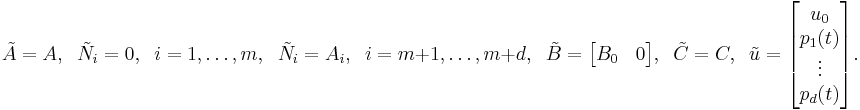
It is important to note that in this way the parameter dependency has been hidden in the structure of a bilinear system and if we use a bilinear model reduction method, we automatically end up with a structure-preserving model reduction method for LPV systems as well. Due to the above mentioned similarity of bilinear and linear control systems, one can generalize some useful and well-known linear concepts. For example, it is possible to extend the method of balanced truncation for bilinear systems. Here, we have to solve generalized Lyapunov equations of the form

$AX+XA^T +\sum_{i=1}^m N_i X N_i^T + BB^T = 0, \qquad A^TY+YA +\sum_{i=1}^m N_i^T Y N_i + C^TC = 0.$

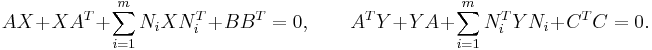
For a detailed analysis of this approach, we refer to e.g. [3]. Another possibility is to aim at a model reduction method which is optimal with respect to a certain system norm. In [1], the authors investigate a possible extension of the linear 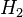$H_2$-norm and propose an algorithm which extends the well-known iterative rational Krylov algorithm (IRKA) to the bilinear setting specified above.

Both methods have been tested on several LPV control systems (e.g., Microthruster Unit and Scanning Electrochemical Microscopy) and seem to be a reasonable alternative to existing parametric model reduction methods.

References

[1] P. Benner and T. Breiten, Interpolation-based H2-model reduction of bilinear control systems, 2011, Preprint MPIMD/11-02.

[2] P. Benner and T. Breiten, On H2-model reduction of linear parameter-varying systems, In Proceedings in Applied Mathematics and Mechanics. Wiley InterScience, 2011.

[3] P. Benner and T. Damm, Lyapunov Equations, Energy Functionals, and Model Order Reduction of Bilinear and Stochastic Systems, SIAM J. Cont. Optim., 49 (2011), pp. 686-711.

Contact information:

Tobias Breiten Vertical Stand