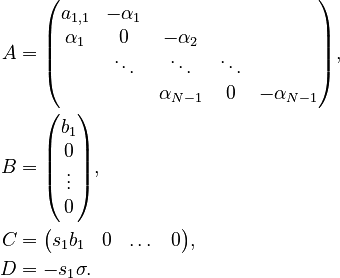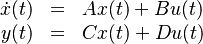Note: This page has not been verified by our editors.
Note: This page has not been verified by our editors.
Description
This procedural benchmark generates an all-pass SISO system based on [1].
For an all-pass system, the transfer function has the property 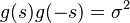 ,
,  ,
or (equivalently) the controllability and observability Gramians are quasi inverse to each other:
,
or (equivalently) the controllability and observability Gramians are quasi inverse to each other: 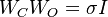 ,
which means this system has a singular Hankel singular value of multiplicity of the system's order.
The system matrices are constructing based on the scheme:
,
which means this system has a singular Hankel singular value of multiplicity of the system's order.
The system matrices are constructing based on the scheme:
We choose 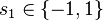 , to be
, to be 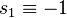 , as this makes the system state-space-anti-symmetric.
Furthermore,
, as this makes the system state-space-anti-symmetric.
Furthermore, 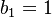 and
and 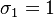 , which makes
, which makes 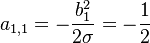 .
.
Data
This benchmark is procedural and the state dimensions can be chosen. Use the following MATLAB code to generate a random system as described above:
function [A,B,C,D] = allpass(N)
% allpass (all-pass system)
% by Christian Himpe, 2020
% released under BSD 2-Clause License
%*
A = gallery('tridiag',N,-1,0,1);
A(1,1) = -0.5;
B = sparse(1,1,1,N,1);
C = -B';
D = 1;
end
The function call requires one argument; the number of states  .
The return value consists of four matrices; the system matrix
.
The return value consists of four matrices; the system matrix  , the input matrix
, the input matrix  , the output matrix
, the output matrix  , and the feed-through matrix
, and the feed-through matrix 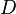 .
.
[A,B,C,D] = allpass(N);
Dimensions
System dimensions:
 ,
,
 ,
,
 ,
,
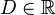 .
.
Citation
To cite this benchmark, use the following references:
- For the benchmark itself and its data:
- The MORwiki Community, All-Pass System. MORwiki - Model Order Reduction Wiki, 2020. http://modelreduction.org/index.php/All_pass_system
@MISC{morwiki_allpass,
author = {{The MORwiki Community}},
title = {All-Pass System},
howpublished = {{MORwiki} -- Model Order Reduction Wiki},
url = {http://modelreduction.org/index.php/All_pass_system},
year = {2020}
}
References
- ↑ R.J. Ober. "Asymptotically Stable All-Pass Transfer Functions: Canonical Form, Parametrization and Realization", IFAC Proceedings Volumes, 20(5): 181--185, 1987.