Introduction
On this page you will find a synthetic parametric model for which one can easily experiment with different system orders  , values of the parameter
, values of the parameter  , as well as different poles and residues.
, as well as different poles and residues.
Also, the decay of the Hankel singular values can be changed indirectly through the parameter  .
.
Model description
The parameter  scales the real part of the system poles, that is,
scales the real part of the system poles, that is, 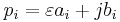 .
For a system in pole-residue form
.
For a system in pole-residue form
we can write down the state-space realisation 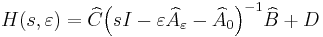 with
with
Notice that the system matrices have complex entries.
For simplicity, assume that  is even,
is even, 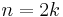 , and that all system poles are complex and ordered in complex conjugate pairs, i.e.
, and that all system poles are complex and ordered in complex conjugate pairs, i.e.
and the residues also form complex conjugate pairs
Then a realization with matrices having real entries is given by
with ![A_{\varepsilon,i} = \left[\begin{array}{cc} a_i& 0 \\ 0 & a_i \end{array}\right]](/morwiki/images/math/c/4/d/c4daf85733e144db5528fb1a97dcc3b1.png) ,
,
![A_{0,i} = \left[\begin{array}{cc} 0& b_i \\ -b_i & 0 \end{array}\right]](/morwiki/images/math/9/c/e/9cefed461140230838eec45e4654af4a.png) ,
,
![B_{i} = \left[\begin{array}{c} 2 \\ 0 \end{array}\right]](/morwiki/images/math/1/6/d/16d6f95252fffc0c7217cb71546f9dff.png) ,
,
![C_{i} = \left[\begin{array}{cc} c_i& d_i\end{array}\right]](/morwiki/images/math/3/b/7/3b78f9392f071a38a8ecf9d7d1af9ee6.png) .
.
Numerical values
We construct a system of order 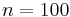 . The numerical values for the different variables are
. The numerical values for the different variables are
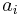 equally spaced in
equally spaced in ![[-10^3, -10]](/morwiki/images/math/0/1/e/01eb0216a83386dce806710ccd49014d.png) ,
,
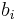 equally spaced in
equally spaced in ![[10, 10^3]](/morwiki/images/math/0/b/e/0be1e9dea133f5e55f228e67a2ea56b4.png) ,
,
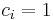 ,
,
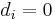 ,
,

![\in [1/50,1]](/morwiki/images/math/3/4/0/3409a13a32f034288c27700bb927d09e.png) .
.
In MATLAB, the system matrices are easily formed as follows:
n = 100; a = -linspace(1e1,1e3,n/2).'; b = linspace(1e1,1e3,n/2).'; c = ones(n/2,1); d = zeros(n/2,1); aa(1:2:n-1,1) = a; aa(2:2:n,1) = a; bb(1:2:n-1,1) = b; bb(2:2:n-2,1) = 0; Ae = spdiags(aa,0,n,n); A0 = spdiags([0;bb],1,n,n) + spdiags(-bb,-1,n,n); B = 2*sparse(mod([1:n],2)).'; C(1:2:n-1) = c.'; C(2:2:n) = d.'; C = sparse(C);
The above system matrices 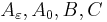 are also available in MatrixMarket format Synth_matrices.tar.gz.
are also available in MatrixMarket format Synth_matrices.tar.gz.
Plots
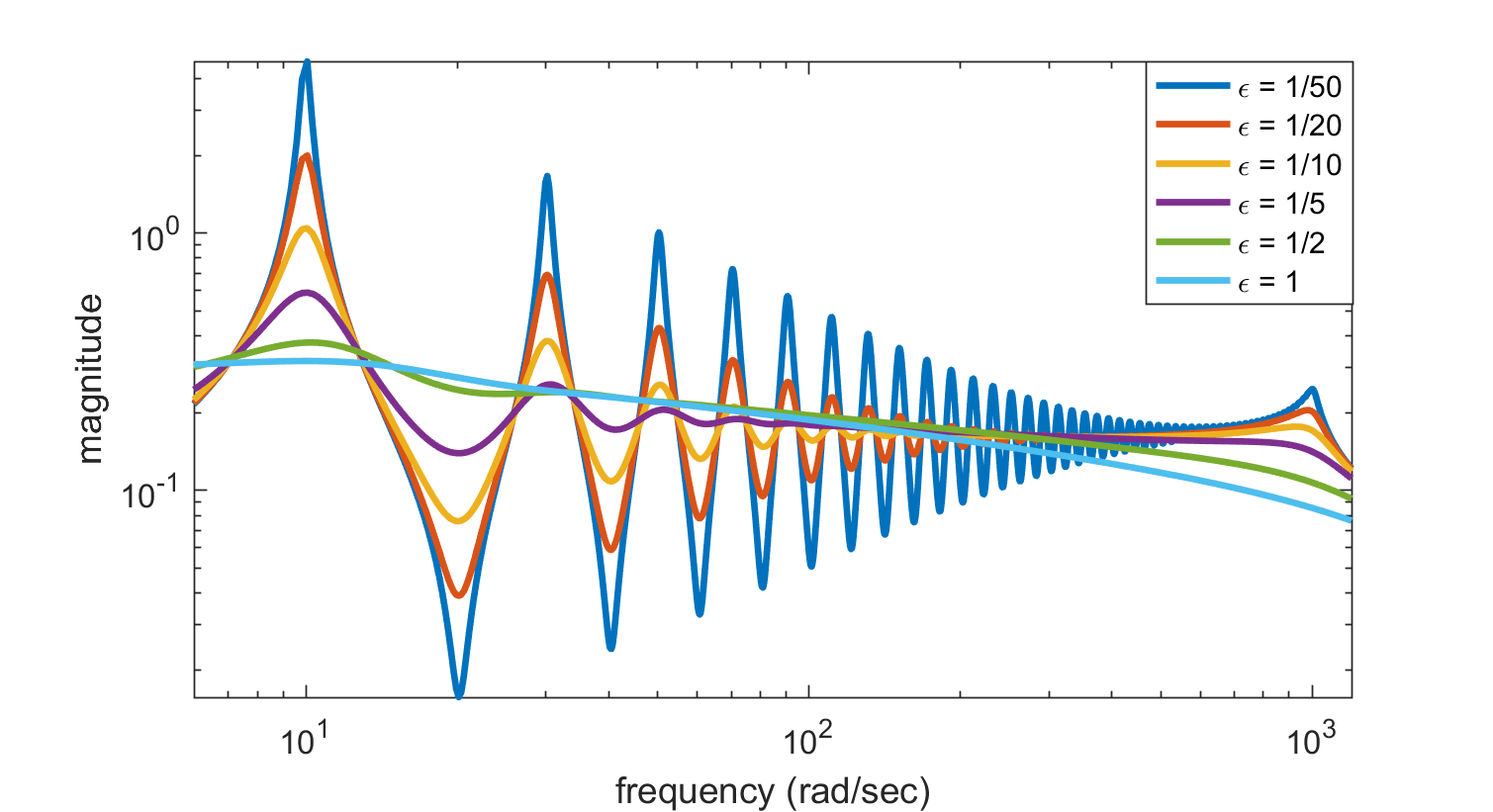
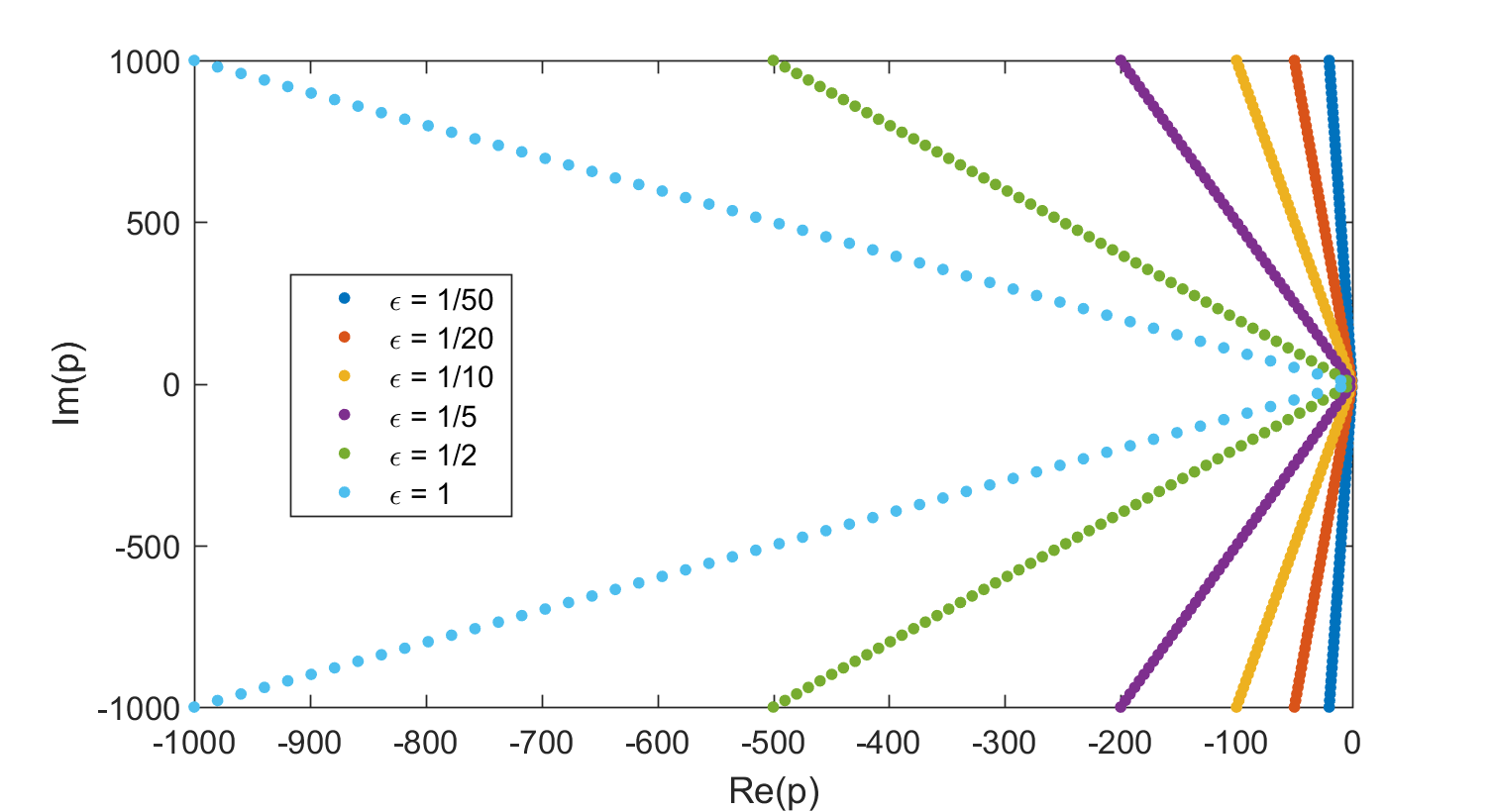
We plot the frequency response and poles for parameter values ![\varepsilon \in [1/50, 1/20, 1/10, 1/5, 1/2, 1]](/morwiki/images/math/1/f/7/1f7392c05a89973f3622df1b8cd09a32.png) .
.
In MATLAB, the plots are generated using the following commands:
r(1:2:n-1,1) = c+1j*d; r(2:2:n,1) = c-1j*d;
ep = [1/50; 1/20; 1/10; 1/5; 1/2; 1]; % parameter epsilon
jw = 1j*linspace(0,1.2e3,5000).'; % frequency grid
for j = 1:length(ep)
p(:,j) = [ep(j)*a+1j*b; ep(j)*a-1j*b]; % poles
[jww,pp] = meshgrid(jw,p(:,j));
Hjw(j,:) = (r.')*(1./(jww-pp)); % freq. resp.
end
figure, loglog(imag(jw),abs(Hjw),'LineWidth',2)
axis tight, xlim([6 1200])
xlabel('frequency (rad/sec)')
ylabel('magnitude')
title('Frequency response for different \epsilon')
figure, plot(real(p),imag(p),'.')
title('Poles for different \epsilon')
Other interesting plots result for small values of the parameter. For example, for 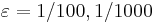 , the peaks in the frequency response become more pronounced, since the poles move closer to the imaginary axis.
, the peaks in the frequency response become more pronounced, since the poles move closer to the imaginary axis.
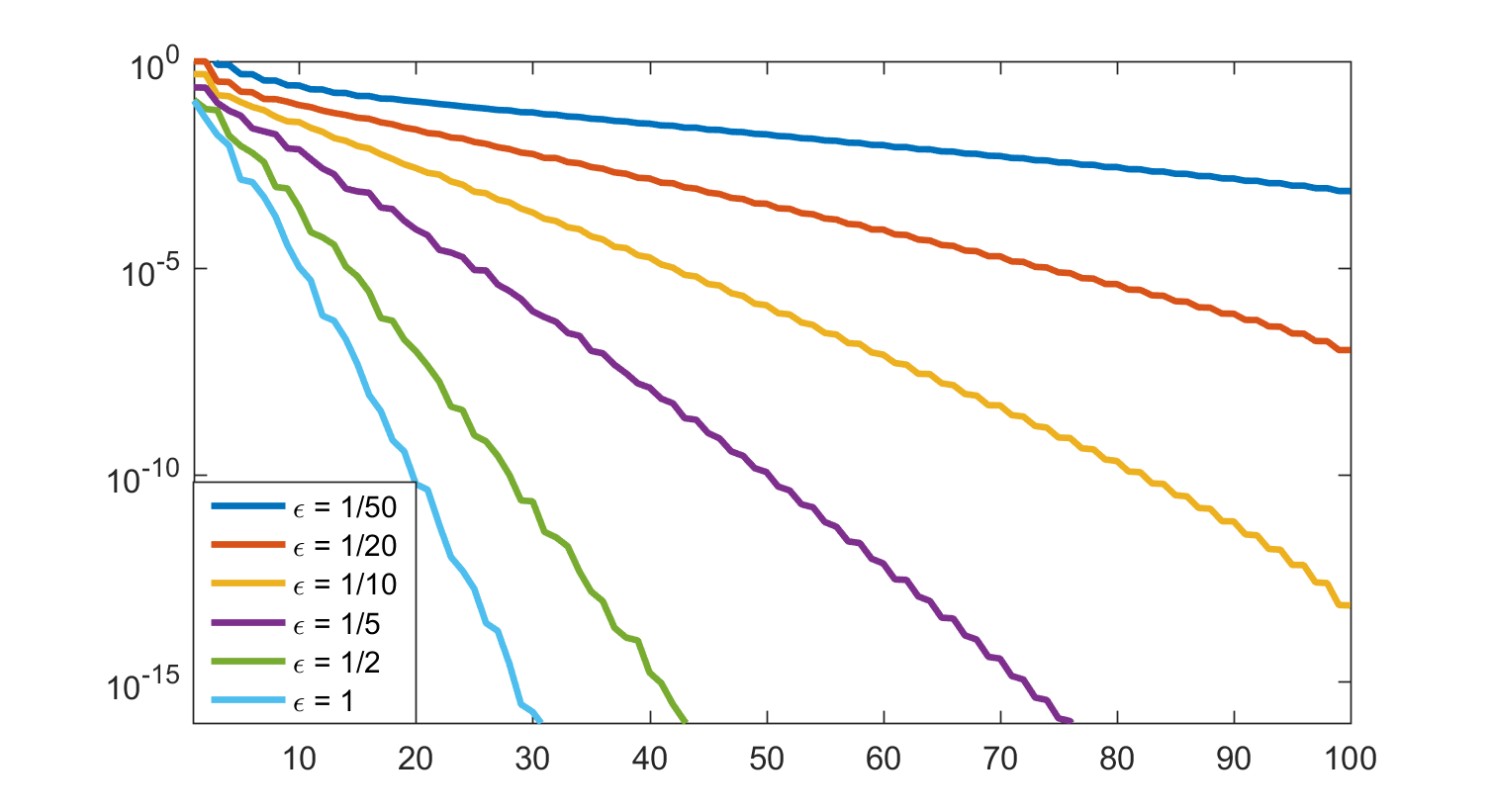
Next, for ![\varepsilon \in [1/50, 1/20, 1/10, 1/5, 1/2, 1]](/morwiki/images/math/1/f/7/1f7392c05a89973f3622df1b8cd09a32.png) , we also plot the decay of the Hankel singular values. Notice that for small values of the parameter, the decay of the Hankel singular values is very slow.
, we also plot the decay of the Hankel singular values. Notice that for small values of the parameter, the decay of the Hankel singular values is very slow.
Antonio Cosmin Ionita 14:20, 29 November 2011 (UTC)

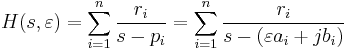
![\varepsilon \widehat{A}_\varepsilon + \widehat{A}_0 = \varepsilon \left[\begin{array}{ccc} a_1 & & \\ & \ddots & \\ & & a_n\end{array}\right] +\left[\begin{array}{ccc} jb_1 & & \\ & \ddots & \\ & & jb_n\end{array}\right] ,](/morwiki/images/math/7/9/0/790c70f3fdd1a7fe269be673f52f5e8c.png)
![\widehat{B} = [1,\ldots,1]^T,\quad \widehat{C} = [r_1,\ldots,r_n],\quad D = 0.](/morwiki/images/math/0/1/9/01952f4b905489c1f4686227dc13e409.png)
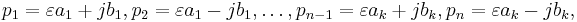
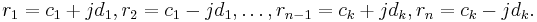
![A_\varepsilon = \left[\begin{array}{ccc} A_{\varepsilon,1} & & \\ & \ddots & \\ & & A_{\varepsilon,k}\end{array}\right], \quad A_0 = \left[\begin{array}{ccc} A_{0,1} & & \\ & \ddots & \\ & & A_{0,k}\end{array}\right], \quad B = \left[\begin{array}{c} B_1 \\ \vdots \\ B_k\end{array}\right], \quad C = \left[\begin{array}{ccc} C_1 & \cdots & C_k\end{array}\right], \quad D = 0,](/morwiki/images/math/f/2/4/f24f26251cc0c24bed73a958735c4681.png)