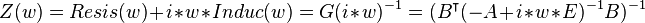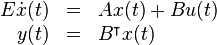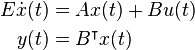Note: This page has not been verified by our editors.
Note: This page has not been verified by our editors.
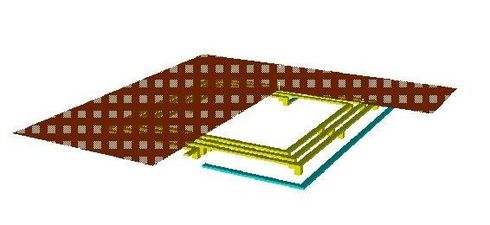
Description: Spiral Inductor PEEC Model
The description of the PEEC model of a spiral inductor can be found in LiKamon.pdf.
The complex impedance is:
A plots of 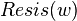 can be found in Rspiral_skin.pdf and a plot of
can be found in Rspiral_skin.pdf and a plot of 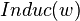 in Lspiral_skin.pdf.
in Lspiral_skin.pdf.
Origin
This benchmark is part of the Oberwolfach Benchmark Collection[1]; No. 38891, see [2].
Data
The model is of order 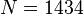 and of the form:
and of the form:
and can be downloaded as spiral_inductor_peec.tar.gz (10.5 MB).
Short Matlab files to:
- plot
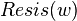 and
and 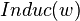 ,
, - perform a PRIMA reduction of order 50,
- produce symmetrized standard state-space system:
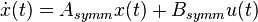 ,
, 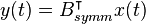 , where
, where 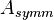 is symmetric.
is symmetric.
can be found in plot_spiral.tar.gz
Dimensions
System structure:
System dimensions:
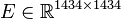 ,
,
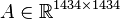 ,
,
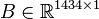 .
.
References
- ↑ J.G. Korvink, E.B. Rudnyi, Oberwolfach Benchmark Collection, Dimension Reduction of Large-Scale Systems, Lecture Notes in Computational Science and Engineering, vol 45: 311--315, 2005.
- ↑ J.R. Li, M. Kamon, Model of a Spiral Inductor Generated by Fasthenry. In: Dimension Reduction of Large-Scale Systems. Lecture Notes in Computational Science and Engineering, vol 45: 373--377, 2005.