Description
The Inverse Lyapunov Procedure (ilp) is a synthetic random linear system generator. It is based on reversing the Balanced Truncation procedure and was developed in [1], where a description of the algorithm is given. In aggregate form, for randomly generated controllability and observability gramians, a balancing transformation is computed. The balanced gramian is the basis for an associated state-space system, which is determined by solving a Lyapunov equation and then unbalanced. A central point is the solution of the Lyapunov equations for the system matrix instead of the gramian matrix. This is feasable due to the symmetric (semi-)positive definiteness of the gramians and the requirement for a stable system, yet with a non-unique solution.
Implementation
An efficient approach to solving the Lyapunov equation is provided by empirical gramians.
Usage
Use the following matlab code to generate a random system as described above:
function [A B C] = ilp(J,N,O,s,r)
% ilp (inverse lyapunov procedure)
% by Christian Himpe, 2013-2014 ( http://gramian.de )
% released under BSD 2-Clause License ( http://gramian.de/#license )
%*
if(exist('emgr')~=2) disp('emgr framework is required. Download at http://gramian.de/emgr.m'); return; end
if(nargin==5) rand('seed',r); randn('seed',r); end;
% Gramian Eigenvalues
WC = exp( rand(N,1) );
WO = exp( rand(N,1) );
% Gramian Eigenvectors
[P S Q] = svd(randn(N));
% Balancing Transformation
WC = P*diag(WC)*P';
WO = Q*diag(WO)*Q';
[U D V] = svd(WC*WO);
% Input and Output
B = randn(N,J);
if(nargin>=4 && s~=0),
C = B';
else,
C = randn(O,N);
end
% Scale Output Matrix
BB = sum(B.*B,2); % = diag(B*B')
CC = sum(C.*C,1)'; % = diag(C'*C)
SC = sqrt(BB./CC)';
C = bsxfun(@times,C,SC);
% Solve System Matrix
f = @(x,u,p) -D*x+B*u;
g = @(x,u,p) C*x;
A = -emgr(f,g,[J N O],[0 0.01 1],'c') - (1e-13)*eye(N);
% Unbalance System
A = V*A*U';
B = V*B;
C = C*U';
The function call requires three parameters; the number of inputs 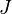 , of states
, of states  and outputs
and outputs 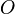 .
Optionally, a symmetric system can be enforced with the parameter
.
Optionally, a symmetric system can be enforced with the parameter  .
For reproducibility, the random number generator seed can be controlled by the parameter
.
For reproducibility, the random number generator seed can be controlled by the parameter  .
The return value consists of three matrices; the system matrix
.
The return value consists of three matrices; the system matrix  , the input matrix
, the input matrix  and the output matrix
and the output matrix  .
.
[A,B,C] = ilp(J,N,O,s,r);
ilp is compatible with MATLAB and OCTAVE and the matlab code can be downloaded from: ilp.m. The Empirical Gramian Framework can be obtained at http://gramian.de.
References
- ↑ S.C. Smith, J. Fisher, "On generating random systems: a gramian approach", Proceedings of the American Control Conference, 2003.
