Inverse_Lyapunov_Procedure
Description
The Inverse Lyapunov Procedure (ilp) is a synthetic random linear system generator. It is based on reversing the Balanced_Truncation procedure and was developed in [1], where a description of the algorithm is given.
A central point is the solution of the Lyapunov equations for the system matrix instead of the gramian matrix. This is feasable due to the symmetric (semi-)positive definiteness of the gramians and the requirement of a stable system. The solution will not be unique and include a symmetric system matrix, yet can be solved efficiently using empirical gramians.
Usage
To generate a random system using the Inverse Lyapunov Procedure download the M-file ilp.m.
The function call requires three parameters; the number of inputs 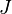 , of states
, of states  and outputs
and outputs 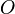 .
Optionally, a symmetric system can be enforced with the parameter
.
Optionally, a symmetric system can be enforced with the parameter 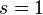 .
The return value consists of three matrices; the system matrix
.
The return value consists of three matrices; the system matrix  , the input matrix
, the input matrix  and the output matrix
and the output matrix  .
.
[A,B,C] = ilp(J,N,O,s);
The required Empirical Gramian Framework can be obtained from http://gramian.de. The ilp generator is compatible with wikipedia:MATLAB MATLAB and wikipedia:GNU_Octave OCTAVE.
References
- ↑ S.C. Smith, J. Fisher, "On generating random systems: a gramian approach", Proceedings of the American Control Conference, 2003.
