All the existing model order reduction (MOR) methods are based on projection. That is to
find a subspace 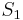 which approximates the manifold where the state
vector
which approximates the manifold where the state
vector 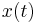 resides. Afterwards,
resides. Afterwards, 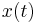 is approximated by a vector
is approximated by a vector 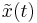 in
in 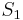 . The reduced model is produced by Petrov-Galerkin projection onto a subspace
. The reduced model is produced by Petrov-Galerkin projection onto a subspace 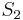 , or by Galerkin projection onto the same subspace
, or by Galerkin projection onto the same subspace 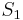 .
.
We use the system
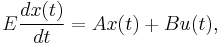
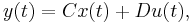
as an example to explain the basic idea. Assuming that an orthonormal
basis 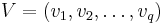 of the subspace
of the subspace 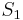 has been
found, then the approximation
has been
found, then the approximation 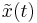 in
in 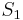 can be represented by
the basis as
can be represented by
the basis as 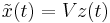 . Therefore
. Therefore 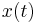 can be approximated by
can be approximated by 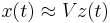 . Here
. Here 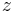 is a vector
of length $q \ll n$.
is a vector
of length $q \ll n$.
Once 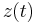 is computed, we can get an
approximate solution
is computed, we can get an
approximate solution 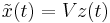 for
for 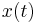 . The vector
. The vector 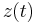 can be computed from the reduced model which is derived by the
following two steps.
can be computed from the reduced model which is derived by the
following two steps.
Step 1. By replacing  in (1) with
in (1) with 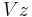 , we get
, we get
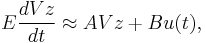
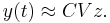
Step 2. The residual is denoted as 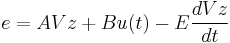 . Force
. Force 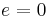 in a properly chosen subspace
in a properly chosen subspace 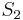 of
of 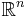 leads to the Petrov-Galerkin projection:
leads to the Petrov-Galerkin projection: 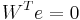 , where the columns of
, where the columns of 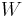 are the basis of
are the basis of  . Finally, the reduced model is
. Finally, the reduced model is
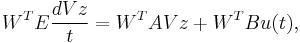
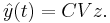
\end{enumerate} % % By defining $\hat{E}=W^TEV$, $\hat {A}=W^TAV$, $\hat{B}=W^TB$, $\hat{C}=CV$, we get the final reduced model % % \begin{equation} \label{sys3} \begin{array}{rcl} \hat{E} \frac{d{\bf z}}{dt}&=&\hat{A}{\bf z}+\hat{B}{\bf u}(t), \\ \hatTemplate:\bf y(t)& = &\hat{C}{\bf z}. \end{array} \end{equation} % % Notice that the approximation $\tilde {\bf x}(t)=V{\bf z}(t)$ of ${\bf x}(t)$ can be obtained from ${\bf z}(t)$ by solving the system in~(\ref{sys3}). The system in~(\ref{sys3}) is much smaller than the system in~(\ref{sys1}) in the sense that there are many less equations in~(\ref{sys3}) than in~(\ref{sys1}). Therefore, the system in~(\ref{sys3}) is much easier to be solved, which is the so-called reduced model. In order to save the simulation time of solving~(\ref{sys1}), the system in~(\ref {sys3}) can be used to replace the original large system in~(\ref{sys1}) to attain a fast simulation. Furthermore, the error between the two systems should be within acceptable tolerance. The error can be measured through the error between the output responses or the transfer functions of the two systems.
