Description
The FitzHugh-Nagumo system describes a prototype of an excitable system (e.g., a neuron).
If the external stimulus 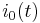 exceeds a certain threshold value, the system will exhibit a characteristic excursion in phase space, before the variables
exceeds a certain threshold value, the system will exhibit a characteristic excursion in phase space, before the variables  and
and 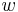 relax back to their rest values. This behaviour is typical for spike generations (=short elevation of membrane voltage
relax back to their rest values. This behaviour is typical for spike generations (=short elevation of membrane voltage  ) in a neuron after stimulation by an external input current.
) in a neuron after stimulation by an external input current.
Here, we present the setting from [1], where the equations for the dynamical system read
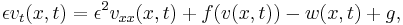
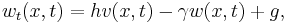
with  and initial and boundary conditions
and initial and boundary conditions
![v(x,0)=0,\quad w(x,0)=0, \quad x\in [0,1],](/morwiki/images/math/a/4/6/a46a8b06dcccd3bdbb094e4acad72a28.png)
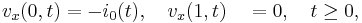
where 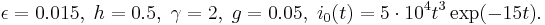 In [1], the previous system of coupled nonlinear PDEs is spatially discretized by means of a finite difference scheme with
In [1], the previous system of coupled nonlinear PDEs is spatially discretized by means of a finite difference scheme with 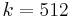 nodes for each PDE. Hence, one obtains a nonlinear (cubic) system of ODEs with state dimension
nodes for each PDE. Hence, one obtains a nonlinear (cubic) system of ODEs with state dimension 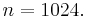
References
Contact information:
