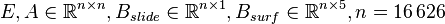1 Description
The vertical stand represents a structural part of a machine tool. On one of its surfaces there are guide rails located. On these rails a tool slide is moving due to the machining process the slide has to perform by the machine tool on top. The machining process produces a certain amount of heat which is transported through the structure into the vertical stand. This heat source is considered to be a temperature input at the guide rails. This transfered heat amount leads to deformations within the device induced by the prevailed temperature field denoted by  . The evolution of this field is modeled by the heat equation
. The evolution of this field is modeled by the heat equation
with the boundary conditions
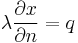 on
on 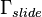 (surface where the tool slide is moving on the guide rails),
(surface where the tool slide is moving on the guide rails),
describing the heat transfer between the tool slide and the vertical stand and
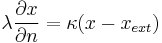 on
on 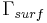 (remaining boundaries),
(remaining boundaries),
which describes the heat transfer to the ambience.
The heat load  induced by the slide and the external temperature
induced by the slide and the external temperature 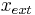 serve as the input
serve as the input  of the corresponding state-space system.
of the corresponding state-space system.
The position of the moving slide has been included into the system as a parameter dependency 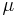 . Due to this motion the boundary
. Due to this motion the boundary 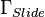 , where the input acts on the system is varying. Thus, the system matrix
, where the input acts on the system is varying. Thus, the system matrix  and the input matrix
and the input matrix  become parameter dependent.
become parameter dependent.
Finally, the system describing the heat evolution induced by the moving heat source is given by:
where
The quantity 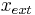 can be assumed as a vector including different ambient temperatures corresponding to different locations of the geometry.
can be assumed as a vector including different ambient temperatures corresponding to different locations of the geometry.
2 Acknowledgement & Origin
This model was developed and investigated[1],[2] in the Collaborative Research Centre Transregio 96 Thermo-Energetic Design of Machine Tools funded by the Deutsche Forschungsgemeinschaft .
3 Data
The data file Data_VertStand.tar.gz contains a MAT_File matrices.mat which consists of the matrices
in sparse format and a file with the coordinates of the mesh nodes called coord.txt.
Here 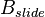 consists of all nodes located on the guide rails.
consists of all nodes located on the guide rails.
In order to get a parameter dependent matrix
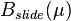 one has to pick the "active" nodes (nodes hit by tool carriage) at vertical position
one has to pick the "active" nodes (nodes hit by tool carriage) at vertical position 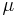 .
The "active" nodes are in the interval of
.
The "active" nodes are in the interval of ![[\mu-\frac{d}{2},\mu+\frac{d}{2}]](/morwiki/images/math/a/7/1/a71f92fd4be99066106491025fe32ad6.png) , where
, where 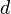 is the heigth of the slide.
Therefore the file coord.txt is provided in Data_VertStand.tar.gz.
is the heigth of the slide.
Therefore the file coord.txt is provided in Data_VertStand.tar.gz.
This file includes a column with indices followed by three additional columns containing the spatial coordinates 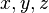 of the corresponding nodes.
of the corresponding nodes.
The matrix 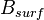 describes the locations where the external temperatures act on.
The first column is responsible for the input of the temperature at the clamped bottom slice of the structure.
Column 2 describes the ... part of the stand. Columns 3 to 5 describe different thresholds with respect to the height of ambient air temperature.
The third column includes the nodes of the lower third
describes the locations where the external temperatures act on.
The first column is responsible for the input of the temperature at the clamped bottom slice of the structure.
Column 2 describes the ... part of the stand. Columns 3 to 5 describe different thresholds with respect to the height of ambient air temperature.
The third column includes the nodes of the lower third ![(y\in[0,670]mm)](/morwiki/images/math/1/5/d/15dadca59513158985b43620edf4027d.png) of the stand.
In column 4 all nodes of the middle third
of the stand.
In column 4 all nodes of the middle third ![(y\in[670,1\,340]mm)](/morwiki/images/math/2/c/9/2c9a274d1a4bd2fbdccd192cb8b8ca06.png) of the geometry are contained
and the fifth column of
of the geometry are contained
and the fifth column of 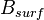 includes the missing upper
includes the missing upper ![(y\in[1\,340,2\,010]mm)](/morwiki/images/math/8/f/7/8f7ee61fb31ab9462369fff516b9d051.png) part.
part.
To clarify this partitioning the geometrical data is given as follows:
Width ( direction):
direction): 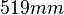 ,
Height (
,
Height (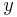 direction):
direction): 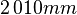 ,
Depth (
,
Depth (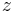 direction):
direction): 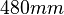
4 References
- ↑ N. Lang, J. Saak, P.Benner, Model Order Reduction for Thermo-Elastic Assembly Group Models , In: Thermo Energetic Design of Machine Tools, Lecture Notes in Production Engineering, 85-92, 2015
- ↑ A. Galant, K. Großmann, A. MühlThermo-Elastic Simulation of Entire Machine Tool , In: Thermo Energetic Design of Machine Tools, Lecture Notes in Production Engineering, 69-84, 2015


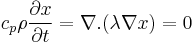
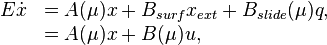
![\begin{array}{lll}
B(\mu)&=[B_{surf}, B_{slide}(\mu)],\\
u&=[x_{ext}^T,q]^T.\\
\end{array}](/morwiki/images/math/4/b/0/4b06d8ab772cfd529264662f29fcdf3a.png)