 Note: This page has not been verified by our editors.
Note: This page has not been verified by our editors.
Description
The flexible space structure benchmark[1] is a procedural modal model which represents structural dynamics with a selectable number actuators and sensors.
Model
In modal form the flexible space structure model for 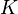 modes,
modes,  actuators and
actuators and  sensors is of second order and given by:
sensors is of second order and given by:
- Failed to parse (syntax error): \ddot{\nu}(t) &= (2 \xi \circ \omega) \circ \dot{\nu}(t) + (\omega \circ \omega) \circ \nu = Bu(t) \\ y(t) &= C_r\dot{\nu}(t) + C_d\nu(t)
with the parameters 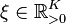 (damping ratio),
(damping ratio), 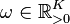 (natural frequency) and using the Hadamard product $\circ$.
The first order representation follows for
(natural frequency) and using the Hadamard product $\circ$.
The first order representation follows for 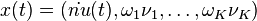 by:
by:
- Failed to parse (syntax error): \dot{x}(t) &= Ax(t) + Bu(t) \\ y(t) &= Cx(t)
with the matrices:
- Failed to parse (syntax error): A := \begin{pmatrix} A_1 & & \\ & \ddots & \\ & & A_K \end{pmatrix}, \\ B := \begin{pmatrix} B_1 \\ \vdots \\ B_K \end{pmatrix}, \\ C := \begin{pmatrix} C_1 & \dots & C_K \end{pmatrix},
and their components:
- Failed to parse (syntax error): A_k := \begin{pmatrix} -2\xi_k\omega_k & -\omega_k \\ \omega_k & 0 \end{pmatrix}, \\ B_k := \begin{pmatrix} b_k \\ 0 \end{pmatrix}, \\ C_k := \begin{pmatrix} c_{rk} & \frac{c_{dk}}{\omega_k} \end{pmatrix},
where 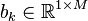 and
and 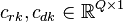 .
.
Benchmark Specifics
For this benchmark the system matrix is block diagonal and thus chosen to be sparse.
The parameters 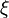 and math>\omega</math> are sampled from a uniform random distributions Failed to parse (syntax error): \mathcal{U}_[0,\frac{1}{1000}]}^K
and Failed to parse (syntax error): \mathcal{U}_[0,100]}^K
respectively.
The components of the input matrix
and math>\omega</math> are sampled from a uniform random distributions Failed to parse (syntax error): \mathcal{U}_[0,\frac{1}{1000}]}^K
and Failed to parse (syntax error): \mathcal{U}_[0,100]}^K
respectively.
The components of the input matrix 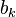 are sampled form a uniform random distribution
are sampled form a uniform random distribution ![\mathcal{U}_{[0,1]}](/morwiki/images/math/8/9/1/8914ff20760d02f585b13a7a84bf17e7.png) ,
while the output matrix
,
while the output matrix  is sampled from a uniform random distribution
is sampled from a uniform random distribution ![\mathcal{U}^{}_[0,10]](/morwiki/images/math/3/9/9/399ba46973f16420bd6eed7c2dc9e965.png) completely w.l.o.g, since if the components of
completely w.l.o.g, since if the components of 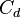 are random their scaling can be ignored.
are random their scaling can be ignored.
Data
The following Matlab code assembles the above described  ,
,  and
and  matrix for a given number of modes
matrix for a given number of modes 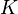 .
.
function [A,B,C] = fss(K,M,Q)
rand('seed',1009);
xi = rand(1,K)*0.001; % Sample damping ratio
omega = rand(1,K)*100; % Sample natural frequencies
A_k = cellfun(@(p) sparse([-2.0*p(1)*p(2),-p(2);p(2),0]), ...
num2cell([xi;omega],1),'UniformOutput',0);
A = blkdiag(A_k{:});
B = kron(rand(K,M),[1;0]);
C = 10.0*rand(Q,2*K);
end
Reference
- ↑ W. Gawronski and T. Williams, "Model Reduction for Flexible Space Structures", Journal of Guidance 14(1): 68--76, 1991
