Description
An anemometer, a flow sensing device, consists of a heater and temperature sensors before and after the heater, placed either directly in the flow or in its vicinity. They are located on a membrane to minimize heat dissipation through the structure. Without any flow, the heat dissipates symmetrically into the fluid. This symmetry is disturbed if a flow is applied to the fluid, which leads to a convection on the temperature field and therefore to a difference between the temperature sensors (see Fig.1 below) from which the fluid velocity can be determined.
The physical model can be expressed by the convection-diffusion partial differential equation[4]:
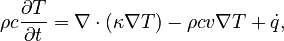
where  denotes the mass density,
denotes the mass density,  is the specific heat,
is the specific heat,
 is the thermal conductivity,
is the thermal conductivity,  is the fluid
velocity,
is the fluid
velocity,  is the temperature and
is the temperature and  the heat flow into the system
caused by the heater.
the heat flow into the system
caused by the heater.
The solid model has been generated and meshed in ANSYS.
Triangular PLANE55 elements have been used for meshing and discretizing by the finite element
method. The order of the system is  .
.
Example with 1 parameter:
The  dimensional ODE system has the following transfer function
dimensional ODE system has the following transfer function
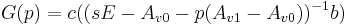
with the fluid velocity ![p(=v) \in [0, 1]](/morwiki/images/math/6/d/7/6d7eded5ef677ead86fc43e11cef17db.png) as single parameter.
Here
as single parameter.
Here  is the heat capacitance matrix,
is the heat capacitance matrix, 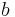 is the load vector which is derived from separating the spatial and temporal variables in
is the load vector which is derived from separating the spatial and temporal variables in  and the FEM discretization w.r.t. the spatial variables.
and the FEM discretization w.r.t. the spatial variables.  are the stiffness matrices with
are the stiffness matrices with 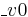 for pure diffusion,
for pure diffusion, 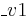 diffusion and convection. Thus, for obtaining pure convection you have to compute
diffusion and convection. Thus, for obtaining pure convection you have to compute 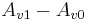 .
.
Example with 3 parameters:
Here, all fluid properties were identified as parameters. Thus, we consider the following transfer function
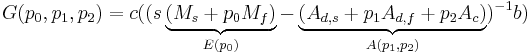
with parameters ![p_0 \in [0, 1], p_1\in [0.1, 2], p_2 \in [1, 2]](/morwiki/images/math/8/2/4/82412b839b31ef17f26c53e869609f35.png) which are combination of the original fluid parameters
which are combination of the original fluid parameters 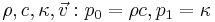 and
and  [5].
[5].
Provenance
IMTEK Freiburg, group of Jan Korvink
data information
Matrices are in the Matrix Market format. The matrix name is used as an extension of the matrix file. The system matrices have been extracted from ANSYS models by means of mor4fem. For more information about permutation, computing the matrices, output, look into readme.txt.
Example with 1 parameter:
Failed to parse (syntax error): *.B & load vector *.E & damping matrix *.C & permutation matrix *.A & stiffness matrices \_v0 & diffusion \_v1 & diffusion and convection
Example with 3 parameters:
\begin{table}[h!]
\begin{tabular}{ll}
- .B & load vector\\
- .E & damping matrices (2)\\
- .A & stiffness matrices (5)\\
\end{tabular} \end{table}
\section{related paper}
\smallskip \renewcommand{\refname}{\bf \normalsize a) About the anemometer}
\begin{thebibliography}{50}
\bibitem{Ern01} H. Ernst. \newblock High-Resolution Thermal Measurements in Fluids. \newblock PhD thesis, University of Freiburg, Germany(2001).
\bibitem{BenMS05} P. Benner and V. Mehrmann and D. Sorensen. \newblock Dimension Reduction of Large-Scale Systems. \newblock {\em Lecture Notes in Computational Science and Engineering}, Springer-Verlag, Berlin/Heidelberg, Germany, 45, 2005.
\bibitem {MooG05cross}
C. Moosmann and A. Greiner.
\newblock Convective Thermal Flow Problems.
\newblock Chapter 16 (pages 341--343) of \cite{BenMS05}
\newcounter{nr} \setcounter{nr}{\value{enumiv}} \end{thebibliography}
\renewcommand{\refname}{\bf \normalsize b) MOR for non-parametrized anemometer} \begin{thebibliography}{10}
\setcounter{enumiv}{\value{nr}}
\bibitem{MooRGetal04}
C. Moosmann, E. B. Rudnyi, A. Greiner, J. G. Korvink.
\newblock Model Order Reduction for Linear Convective Thermal Flow.
\newblock {\em Proceedings of 10th International Workshops on THERMal INvestigations of ICs and Systems}, THERMINIC2004, 29 Sept - 1 Oct , 2004,
Sophia Antipolis, France.
\setcounter{nr}{\value{enumiv}} \end{thebibliography}
\renewcommand{\refname}{\bf \normalsize c) MOR for parametrized anemometer} \begin{thebibliography}{10}
\setcounter{enumiv}{\value{nr}}
\bibitem{BauBGKLM11}
U.~Baur, P.~Benner, A.~Greiner, J.~G. Korvink, J.~Lienemann und C.~Moosmann.
\newblock Parameter preserving model order reduction for {MEMS} applications.
\newblock {\em {MCMDS} Mathematical and Computer Modelling of Dynamical Systems}, 17(4):297--317, 2011.
\bibitem{ThesisMoosmann07} %??? C. Moosmann. \newblock {\em {ParaMOR} - Model Order Reduction for parameterized MEMS
applications}.
\newblock PhD thesis, University of Freiburg, Germany(2007).
%Nanotech.pdf \bibitem{MooRGetal05} C. Moosmann, E. B. Rudnyi, A. Greiner, J. G. Korvink, M. Hornung. \newblock Parameter preserving Model Order Reduction of a Flow Meter. \newblock {\em Technical Proceedings of the 2005 Nanotechnology Conference and Trade Show}, Nanotech 2005, May 8-12, 2005, Anaheim, California, USA, NSTINanotech 2005, vol. 3, p. 684-687.
%rudnyi06mathmod.pdf auch electrochem microscop
\bibitem{RudMGetal06}
E. B. Rudnyi, C. Moosmann, A. Greiner, T. Bechtold, J. G. Korvink.
\newblock Parameter Preserving
Model Reduction for MEMS System-level Simulation and Design.
\newblock {\em Proceedings of MATHMOD 2006}, February 8 -
10, 2006, Vienna University of Technology, Austria.
