Description
Model truncation is one of the oldest MOR methods for linear time invariant systems
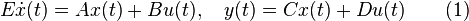
The main idea is to construct the projection matrices as ![V=[x_1,\ldots,x_r], W=[y_1,\ldots,y_r]](/morwiki/images/math/0/e/e/0ee65b7c5e9ab333049a1b288dac26d0.png) where the
where the 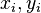 are right and left eigenvectors corresponding to
certain eigenvalues
are right and left eigenvectors corresponding to
certain eigenvalues 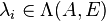 . The eigentriples
. The eigentriples 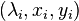 satisfy.
satisfy.
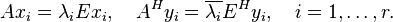
They are different ways to select this typically small subset of eigenvalues. An often used criterion is to take the eigenvalue closest to the imaginary axis, i.e. the ones with the smallest real part, and their associated eigenvectors into account. Dominant pole based modal truncation selects 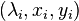 with respect to their contribution in the transfer function and is described below.
with respect to their contribution in the transfer function and is described below.
One advantage of such eigenvalue based MOR methods is that they can be easily adapted to more general time invariant systems, for instance, systems in second order form
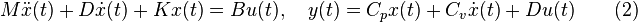
which occur frequently in vibration analysis for mechanical systems. There, 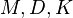 being referred to as Mass, Damping, and Stiffness matrix are represent a finite element discretization of the mechanical system. In fact, a large variety of modal truncation type approaches originated in this application[1], e.g., Condensation (Guyan reduction)[2] and Component Mode Synthesis (Craig-Bampton)[3].
Modal truncation methods can also be generalized to handle linear, time-invariant system with higher time derivatives and even with time-delays, e.g.
being referred to as Mass, Damping, and Stiffness matrix are represent a finite element discretization of the mechanical system. In fact, a large variety of modal truncation type approaches originated in this application[1], e.g., Condensation (Guyan reduction)[2] and Component Mode Synthesis (Craig-Bampton)[3].
Modal truncation methods can also be generalized to handle linear, time-invariant system with higher time derivatives and even with time-delays, e.g.
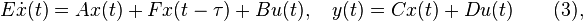
where 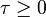 is the time-delay.
is the time-delay.
Other advantages are that modal truncation can in principle applied to DAEs of arbitrary index and to unstable systems. They do, however, preserve stability since they do not change the eigenvalues of the original system. They rely on eigenvalue algorithms to compute the required eigentriplets. There are several algorithms available for this purpose for large and sparse matrices.
Disadvantages are the lack of a computationally feasible error bound and the often observed lower approximation accuracy compared to other MOR methods.
Dominant pole based modal truncation
This modal truncation variant aims at the identification of eigentriplets 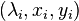 which have a strong contribution to the input-output behavior of the dynamical. For this purpose, let all eigenvalues be semisimple and consider the residue expansion of the transfer function matrix (exemplary of (1))
which have a strong contribution to the input-output behavior of the dynamical. For this purpose, let all eigenvalues be semisimple and consider the residue expansion of the transfer function matrix (exemplary of (1))
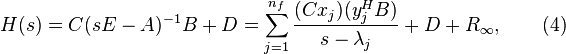
where 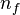 is the number of finite eigenvalue of
is the number of finite eigenvalue of 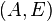 and
and 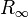 is the residue corresponding to the infinite eigenvalues. For simplicity we assume
is the residue corresponding to the infinite eigenvalues. For simplicity we assume 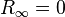 . The quantities
. The quantities 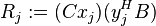 in the numerator of the above series are the residues w.r.t.
in the numerator of the above series are the residues w.r.t. 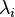 . Each finite eigenvalue
. Each finite eigenvalue 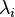 is pole of
is pole of 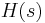 and is called dominant pole if its scaled residue norm
and is called dominant pole if its scaled residue norm
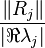 is larger than the ones of the other eigentriples which corresponds in some sense to the largest summand in the residue expansion of
is larger than the ones of the other eigentriples which corresponds in some sense to the largest summand in the residue expansion of 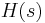 . Dominant poles can be observed in the Bode, or sigma plot of
. Dominant poles can be observed in the Bode, or sigma plot of 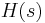 where peaks occur near the imaginary part of the dominant eigenvalue.
where peaks occur near the imaginary part of the dominant eigenvalue.
Dominant pole based model truncation then amounts to computed the, say 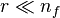 , most dominant poles (i.e., the dominant eigentriplets) and
take the associated right and left eigenvectors as columns of the truncation matrices
, most dominant poles (i.e., the dominant eigentriplets) and
take the associated right and left eigenvectors as columns of the truncation matrices 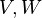 . Equivalently, the reduced order model is obtained by truncating the residue expansion (4):
. Equivalently, the reduced order model is obtained by truncating the residue expansion (4):
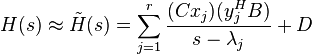 .
.
Note that 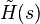 constructed in that way is often called modal equivalent of
constructed in that way is often called modal equivalent of 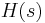 .
A specially tailored eigenvalue algorithm to compute the sought dominant eigentriplets for this task is the (Subspace Accelerated) Dominant Pole Algorithm.
[4]
[5]
[6]
[7]
[8]
A MATLAB implementation of this algorithms and certain variants of thereof can be found at https://sites.google.com/site/rommes/software.
.
A specially tailored eigenvalue algorithm to compute the sought dominant eigentriplets for this task is the (Subspace Accelerated) Dominant Pole Algorithm.
[4]
[5]
[6]
[7]
[8]
A MATLAB implementation of this algorithms and certain variants of thereof can be found at https://sites.google.com/site/rommes/software.
References
- ↑ P. Koutsovasilis and M. Beitelschmidt, "Comparison of Model Reduction Techniques for Large Mechanical Systems", Multibody System Dynamics, vol.20, no.2, pp.111-128, 2008
- ↑ R.J. Guyan, "Reduction of Stiffness and Mass Matrices", AIAA Journal, vol.3, no.2, pp.380, 1965
- ↑ R. Craig and M. Bampton, "Coupling of Substructures for Dynamic Analyses", AIAA Journal, vol.6, no.7, pp.1313-1319, 1968
- ↑ N. Martins, L. Lima, and H. Pinto, "Computing dominant poles of power system transfer functions", IEEE Transactions on Power Systems, vol.11, no.1, pp.162-170, 1996
- ↑ J. Rommes and N. Martins, "Efficient computation of transfer function dominant poles using subspace acceleration", IEEE Transactions on Power Systems, vol.21, no.3, pp.1218-1226, 2006
- ↑ J. Rommes and N. Martins, "Efficient computation of multivariable transfer function dominant poles using subspace acceleration", IEEE Transactions on Power Systems, vol.21, no.4, pp.1471-1483, 2006
- ↑ J. Rommes, "Methods for eigenvalue problems with applications in model order reduction", Ph.D. dissertation, Universiteit Utrecht, 2007.
- ↑ P. Kürschner, "Two-sided eigenvalue methods for modal approximation”, Master’s thesis, Chemnitz University of Technology, Department of Mathematics, Germany, 2010.
