This is an extension of the non-parametrized model of Gas sensor in the Oberwolfach Model Reduction Benchmark Collection (http://simulation.uni-freiburg.de/downloads/benchmark Gas sensor(38880)) to a parametrized model.
Description of the device
There is a large demand for gas sensing devices in various domains. They are desired in e. g. safety applications where combustible or toxic gases are present or in comfort applications, such as climate controls of buildings and vehicles where good air quality is required. Additionally, gas monitoring is needed in process control and laboratory analytics. All of these applications demand cheap, small and user-friendly gas sensing devices which show high sensitivity, selectivity and stability with respect to a given application.
A micromachined gas sensor is not only a challenge with respect to thermal design but also with respect to mechanical design. Only by choosing the right mechanical design a large intrinsic or thermal-induced membrane stress leading to membrane deformation/ breaking of the membrane can be avoided. It is further necessary to build a chemometrics calibration model which correlates the set of sensor resistance measurements to the sensed gas concentration. Prior to fabrication, a thermal simulation is performed to determine the heating efficiency and temperature homogeneity of the gas sensitive regions. As the device is connected to circuitry for heating power control and sensing resistor readout, a system-level simulation is also needed. Hence, a compact thermal model must be generated. (The text above is taken from [1].)
Description of the model
The heat transfer within a hotplate is described through the governing heat transfer equation [2]
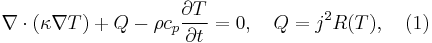
where 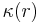 is the thermal conductivity in
is the thermal conductivity in  at the position
at the position  is the
specific heat capacity in
is the
specific heat capacity in 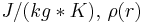 is the mass density in
is the mass density in
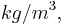 and
and 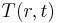 is the temperature distribution. We assume a
homogeneous heat generation rate over a lumped resistor:
is the temperature distribution. We assume a
homogeneous heat generation rate over a lumped resistor:

with unit 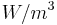 .
We use the initial condition
.
We use the initial condition 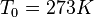 , and the
Dirichlet boundary condition
, and the
Dirichlet boundary condition 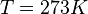 at the bottom of
the computational domain. The convection boundary condition at the top of the membrane is
at the bottom of
the computational domain. The convection boundary condition at the top of the membrane is
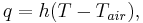
where  is the heat transfer coefficient between the membrane and the ambient air in
is the heat transfer coefficient between the membrane and the ambient air in 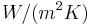 .
.
Assuming 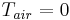 , spatial discretization of the heat transfer model in (1) leads to the parametrized system as below,
, spatial discretization of the heat transfer model in (1) leads to the parametrized system as below,
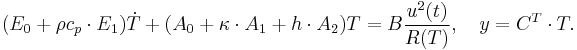
Here 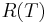 is either a constant heat resistivity
is either a constant heat resistivity 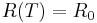 , or
, or 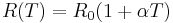 , which depends linearly on the temperature. Here we use
, which depends linearly on the temperature. Here we use 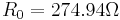 and temperature coefficient
and temperature coefficient 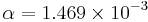 . The model was created and meshed in ANSYS. It contains a constant load vector corresponding to the constant input power of
. The model was created and meshed in ANSYS. It contains a constant load vector corresponding to the constant input power of 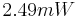 . The number of degrees of freedom is
. The number of degrees of freedom is 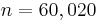 .
.
The input function  is a step function with the value
is a step function with the value 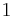 , which disappears at the time
, which disappears at the time 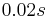 . This means between
. This means between  and
and 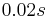 input is one and after that it is zero. However, be aware that
input is one and after that it is zero. However, be aware that  is just a factor with which the load vector B is multiplied and which corresponds to the heating power of
is just a factor with which the load vector B is multiplied and which corresponds to the heating power of 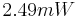 . This means if one keeps
. This means if one keeps  as suggested above, the device is heated with
as suggested above, the device is heated with 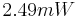 for the time length of 0.02s and after that the heating is turned off. If for whatever reason, one wants the heating power to be
for the time length of 0.02s and after that the heating is turned off. If for whatever reason, one wants the heating power to be 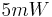 , then
, then  has to be set equal to two, etc...
When
has to be set equal to two, etc...
When 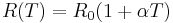 , it is a function of the state vector
, it is a function of the state vector  and hence, the system has non-linear input. (It is also called a weakly nonlinear system.)
and hence, the system has non-linear input. (It is also called a weakly nonlinear system.)
Data information
The system matrices are in MatrixMarket format (http://math.nist.gov/MatrixMarket/) and can be downloaded here File:Matrices gassensor.tgz. The files named by *.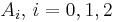 correspond to the system matrices
correspond to the system matrices 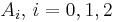 , respectively. The files named by
, respectively. The files named by 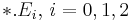 correspond to
correspond to 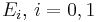 . The file named by
. The file named by 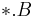 corresponds to the load vector
corresponds to the load vector  and the file named by
and the file named by 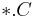 corresponds to the output matrix
corresponds to the output matrix  .
.
References
[1] T. Bechtold, "Model Order Reduction of Electro-Thermal MEMS", PhD thesis, Department of Microsystems Engineering, University of Freiburg, 2005.
[2] T. Bechtold, D. Hohfel, E. B. Rudnyi and M. Guenther, "Efficient extraction of thin-film thermal parameters from numerical models via parametric model order reduction," J. Micromech. Microeng. 20(2010) 045030 (13pp).
