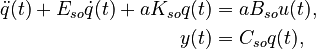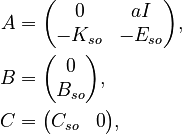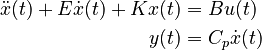Clamped Beam

Clamped Beam

Background
Benchmark ID	clampedBeam_n348m1q1
Category	slicot
System-Class	LTI-FOS
Parameters
nstates	348
ninputs	1
noutputs	1
nparameters	0
components	A, B, C
Copyright
License	NA
Creator	Christian Himpe
Editor	Christian Himpe Petar Mlinarić
Location
NA

Description: Clamped Beam Model

This benchmark models a cantilever beam, which is a beam clamped on one end. More details can be found in and , .

For larger beam-type benchmarks see the linear 1d beam and electrostatic beam benchmarks.

Origin

This benchmark is part of the SLICOT Benchmark Examples for Model Reduction.

Data

The system matrices $A$, $B$, $C$ are available from the SLICOT benchmarks page: beam.zip and are stored as MATLAB .mat file.

Here is Python code for loading the matrices ($A$ is stored as a sparse matrix that is mostly full and $C$ is stored as an array of 8-bit unsigned integers):

import numpy as np
from scipy.io import loadmat

mat = loadmat('beam.mat')
A = mat['A'].toarray()
B = mat['B']
C = mat['C'].astype(np.float64)

The 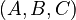$(A, B, C)$ represents a second-order system

$\begin{align} \ddot{q}(t) + E_{so} \dot{q}(t) + a K_{so} q(t) &= a B_{so} u(t), \\ y(t) &= C_{so} q(t), \end{align}$

as

$\begin{align} A &= \begin{pmatrix} 0 & a I \\ -K_{so} & -E_{so} \end{pmatrix}, \\ B &= \begin{pmatrix} 0 \\ B_{so} \end{pmatrix}, \\ C &= \begin{pmatrix} C_{so} & 0 \end{pmatrix}, \end{align}$

where $a \approx 21.3896$.

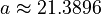Here is Python code for checking the structure and extracting the second-order matrices:

n = 348
n2 = n // 2

assert np.all(A[:n2, :n2] == 0)
assert np.all(A[:n2, n2:] == A[0, n2] * np.eye(n2))
assert np.all(B[:n2] == 0)
assert np.all(C[:, :n2] == 0)

a = A[0, n2]
Eso = -A[n2:, n2:]
Kso = -a * A[n2:, :n2]
Bso = a * B[n2:]
Cso = C[:, :n2]

Dimensions

First differential order

System structure:

$\begin{align} \dot{x}(t) &= A x(t) + B u(t) \\ y(t) &= C x(t) \end{align}$

System dimensions:

$A \in \mathbb{R}^{348 \times 348}$, $B \in \mathbb{R}^{348 \times 1}$, $C \in \mathbb{R}^{1 \times 348}$.

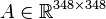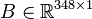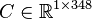Second differential order

System structure:

$\begin{align} \ddot{x}(t) + E \dot{x}(t) + K x(t) &= B u(t) \\ y(t) &= C_p \dot{x}(t) \end{align}$

System dimensions:

$E, K \in \mathbb{R}^{174 \times 174}$, $B \in \mathbb{R}^{174 \times 1}$, $C_p \in \mathbb{R}^{1 \times 174}$.

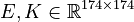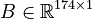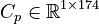Citation

To cite this benchmark, use the following references:

• For the benchmark itself and its data:

Niconet e.V., SLICOT - Subroutine Library in Systems and Control Theory, http://www.slicot.org

@MANUAL{slicot_beam,
 title =        {{SLICOT} - Subroutine Library in Systems and Control Theory},
 organization = {Niconet e.V.}
 address =      {\url{http://www.slicot.org}},
 key =          {SLICOT}
}

• For the background on the benchmark:

@ARTICLE{morAntSG01,
 author =       {A.C. Antoulas, D.C. Sorensen and S. Gugercin},
 title =        {A survey of model reduction methods for large-scale systems},
 journal =      {Contemporary Mathematics},
 volume =       {280},
 pages =        {193--219},
 year =         {2001},
 doi =          {10.1090/conm/280}
}