Fluid Flow Linearized Open Cavity Model

Note: This page has not been verified by our editors.

Description

Motivation

Figure 1: Open cavity geometry.

Figure 2: Open parametric frequency response.

Let us consider the fluid-flow configuration. It consists of a two-dimensional open square cavity flow problem where air flows from left to right for three different Reynolds numbers. Such configuration is described in details in the original work of \cite{Barbagallo:2008} and in \cite{PoussotLPVS:2015}, and illustrated on Figure \ref{fig:ns} (bottom right). For simulating the phenomena, Navier and Stokes equations are used along a mesh composed of $193,874$ triangles, corresponding to $n=680,974$ degrees of freedom for the velocity variables along the $x$ and $y$ axis. After linearization around three fixed points for varying Reynolds numbers $Re=\{4000,5250,6000\}$ and discretisation along the flow axis, three dynamical models $\{\Htran_i\}_{i=1}^3$ can be described as a \textbf{DAE} realisation of order $n=680,974$ where the input $\u(t)$ is the vertical pressure actuator located upstream of the cavity and the output $\y(t)$ is a shear stress sensor, located downstream of the cavity. In this particular case, the parameter is the Reynolds number $Re$. In \cite{PoussotLPVS:2015}, the \textbf{IRKA} approach \cite{GugercinSIAM:2008} (being a realization based $\mathcal H_2$-oriented reduction method) is used to sequentially approximate each realization with a low dimensional one. Then, the interpolation along the parameter is done in a second step by interpolating each coefficients in the canonical basis of the obtained realization.

Here instead, the parametric Loewner framework is applied. First, the frequency response of the three configurations for $N=200$ logarithmically spaced frequencies $\{z_k\}_{k=1}^N=\{\imath \omega_{\overline k},-\imath \omega_{\overline k}\}_{k=1}^{N/2}$ are first computed. Then, ten intermediate configurations between each Reynolds numbers $Re=\{4000,5250,6000\}$ are constructed by linear interpolation. We obtain $\{z_k\}_{k=1}^{N=200}$, $\{p_l\}_{l=1}^{N=31}$ and thus $\Phi \in \IC^{200 \times 31}$. Our objective is to come up with a parametrized linear model that is able to faithfully reproduce the original transfer data on a particular range of frequencies as well as on a target parameter range.

Considered data

The benchmark contains a set of complex-domain reponses provided at varying real frozen Reynolds parametric values. The numerical values data as inspired (but slightly modified) from the reference paper given below and are provided as Matlab data. More specifically, This benchmark contains a set of complex-domain/parametric(real)-domain input-output data computed from a high dimensional linear descriptor model given as (where 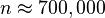$n\approx 700,000$ ):

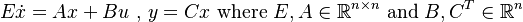
$E \dot x = Ax + Bu \text{ , } y=Cx \text{ where } E,A \in \mathbb R^{n\times n} \text{ and } B,C^T \in \mathbb R^{n}$

and which matrices have been obtained by linearizing the Navier and Stokes equations at frozen Reynolds numbers, from a high fidelity simulator.

The data provided in this use-case are given as the triple:

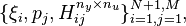
$\{\xi_i,p_j,H_{ij}^{n_y\times n_u}\}_{i=1,j=1}^{N+1,M},$

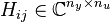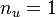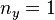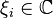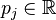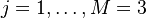where $H_{ij}\in\mathbb C^{n_y\times n_u}$ represents the transfer from $n_u=1$ input signal (upward cavity pressure) to $n_y=1$ measurement output (downward cavity pressure), evaluated at varying complex values $\xi_i\in\mathbb C$ and $p_j\in\mathbb R$ , for $j=1,\dots,M=3$ . Specifically, the frequencies are between 0.1Hz until 42.1Hz in steps of 0.1Hz.

Origin

Collaboration between ONERA DTIS (dynamical systems and information departement) and DAAA (Fluid mechanics departement). The data come from a fluid simulator (coded in FreeFem++). The model is constructed by D. Sipp and post-processing was performed jointly by P. Vuillemin and C. Poussot-Vassal.

Data

Description

Objective

Citation

To cite this benchmark, use the following references:

For the benchmark itself and its data:

The MORwiki Community, Fluid Flow Linearized Open Cavity Model. MORwiki - Model Order Reduction Wiki, 2021. https://morwiki.mpi-magdeburg.mpg.de/morwiki/index.php/Fluid_Flow_Linearized_Open_Cavity_Model

For the background on the benchmark with a dynamical and control engineering point of view:

@inproceedings{PoussotLPVS:2015,
  author    = {C. Poussot-Vassal and  D. Sipp},
  title     = {Parametric reduced order dynamical model construction of a fluid flow control problem},
  booktitle = {Proceedings of the 1st IFAC Workshop on Linear Parameter Varying Systems},
  address   = {Grenoble, France},
  month     = {October},
  year      = {2015},
  pages     = {133-138},
}

For the background on the benchmark with a fluid-flow point of view:

@article{Barbagallo:2008,
  author  = {A. Barbagallo and D. Sipp and P.J. Schmid},
  journal = {Journal of Fluid Mechanics},
  pages   = {1-50},
  title   = {Closed-loop control of an open cavity flow using reduced-order models},
  volume  = {641},
  year    = {2008}
}

References

Contact

Charles Poussot-Vassal