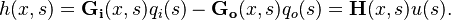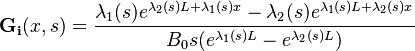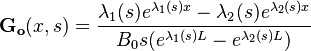Note: This page has not been verified by our editors.
Note: This page has not been verified by our editors.
Description
Motivation
The so-called Saint-Venant equations are largely used in the hydraulic domain to model the dynamics of an open channel flow. These equations consist of two nonlinear hyperbolic PDEs. In the considered benchmark, under mild simplifying assumptions detailed in [1], the St Venant PDE equations describing the height variation  of the river as a function of the inflow
of the river as a function of the inflow 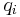 and outflow
and outflow 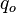 variations, at location
variations, at location  (
(![x\in[0\,\,L]](/morwiki/images/math/9/2/2/922897af4e1e015582f11b61e69808c9.png) ,
, 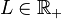 ), obtained around some flow and height linearisation point, can be formulated as follows:
), obtained around some flow and height linearisation point, can be formulated as follows:
The 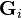 and
and 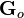 functions are irrational and read
functions are irrational and read
and
Considered data
The benchmark contains the above irrational model description together with the numerical data as used in the reference paper
Origin
Collaboration between ONERA and EDF. The data from the simplified hydro electric open channel model come from V. Dalmas and G. Robert while and the treatment performed jointly with P. Vuillemin, and C. Poussot-Vassal.
Data
Citation
To cite this benchmark, use the following references:
- For the benchmark itself and its data:
- The MORwiki Community, Hydro-Electric Open Channel. MORwiki - Model Order Reduction Wiki, 2018. https://morwiki.mpi-magdeburg.mpg.de/morwiki/index.php/Hydro-Electric_Open_Channel
@inproceedings{DalmasECC:2016,
author = {V. Dalmas and G. Robert and C. Poussot-Vassal and I. {Pontes Duff} and C. Seren},
title = {From infinite dimensional modelling to parametric reduced order approximation: Application to open-channel flow for hydroelectricity},
booktitle = {Proceedings of the 15th European Control Conference},
address = {Aalborg, Denmark},
month = {July},
year = {2016},
pages = {1982-1987},
}
References
Contact
- ↑ V. Dalmas, G. Robert, C. Poussot-Vassal, I. Pontes-Duff and C. Seren, "From infinite dimensional modelling to parametric reduced order approximation: Application to open-channel flow for hydroelectricity", in Proceedings of the European Control Conference (ECC), Aalborg, Denmark, July, 2016, pp. 1982-1987, DOI: https://doi.org/10.1109/ECC.2016.7810582