Parametric model order reduction (PMOR) methods are designed for model order reduction of parametrized systems, where the parameters of the system play an important role in practical applications such as Integrated Circuit (IC) design, MEMS design, Chemical engineering etc.. The parameters could be the variables describing geometrical measurement, material property, damping of the systems or component flow-rate. The reduced models are constructed such that all the parameters can be preserved with acceptable accuracy. Usually the time of simulating the reduced models is much shorter than directly simulating the original large system. However, the time of constructing the reduced model increases with the dimension of the original system. If the original system is very large, the process of obtaining the reduced model could become extremely slow. The recycling algorithm considered in this paper tries to accelerate the above process and reduce the time of deriving the reduced model to a reasonable range.
The method introduced here is from [1][2], and applies to a linear parametrized system, which has the following form in the frequency domain:
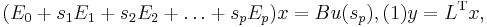
where 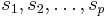 are the parameters of the system. They can be any scalar functions of some source parameters, like
are the parameters of the system. They can be any scalar functions of some source parameters, like 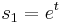 , where
, where 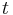 is time, or combination of several physical parameters like
is time, or combination of several physical parameters like 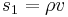 , where
, where  and
and  are two physical parameters.
are two physical parameters.
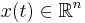 is the state vector,
is the state vector, 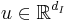 and
and 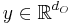 are, respectively, the inputs and outputs of the
system. To obtain the reduced model in (1), a
projection matrix
are, respectively, the inputs and outputs of the
system. To obtain the reduced model in (1), a
projection matrix 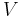 which is independent of all the parameters has
to be computed.
which is independent of all the parameters has
to be computed.
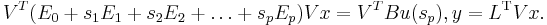
The matrix $V$ is derived by orthogonalizing a number of moment matrices of the system in (1)[1][2].
By defining 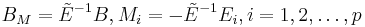 and
and
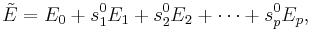
we can expand  in (1) at
in (1) at 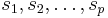 around a set of
expansion points
around a set of
expansion points ![p_0=[s_1^0,s_2^0,\cdots,s_p^0]](/morwiki/images/math/4/1/3/413a7d9006408a35467750f81e49d248.png) as below,
as below,
![x=[I-(\sigma_1M_1+\ldots +\sigma_pM_p]^{-1}B_Mu(s_p)
=\sum\limits_{i=0}^{\infty}(\sigma_1M_1+\ldots+\sigma_pM_p)^iB_Mu(s_p).](/morwiki/images/math/f/8/b/f8bf6e51fa587497870a6861474ec83c.png)
Here 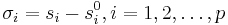 . We call the coefficients
in the above series expansion moment matrices of the parametrized
system, i.e.
. We call the coefficients
in the above series expansion moment matrices of the parametrized
system, i.e. 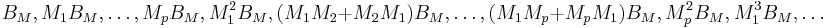 . The corresponding moments are those moment
matrices multiplied by
. The corresponding moments are those moment
matrices multiplied by  from the left. The matrix
from the left. The matrix 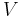 can be
generated by first explicitly computing some of the moment matrices
and then orthogonalizing them as is suggested in~\cite{Daniel04}.
The resulting
can be
generated by first explicitly computing some of the moment matrices
and then orthogonalizing them as is suggested in~\cite{Daniel04}.
The resulting 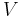 is desired to expand the subspace:
is desired to expand the subspace:
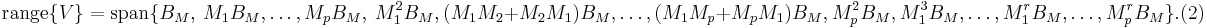
However, 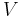 does not really span the whole subspace, because the
latterly computed vectors in the subspace become linearly dependent
due to numerical instability. Therefore, with this matrix
does not really span the whole subspace, because the
latterly computed vectors in the subspace become linearly dependent
due to numerical instability. Therefore, with this matrix 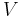 one
cannot get an accurate reduced model which matches all the moments
included in the subspace.
one
cannot get an accurate reduced model which matches all the moments
included in the subspace.
Instead of directly computing the moment matrices in (2)[1], a
numerically robust method is proposed in [1] (the
detailed algorithm is described in [3]), which combines
the recursions in (4) with the modified Gram-Schmidt
process to implicitly compute the moment matrices. The computed 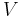 is actually an orthonormal basis of the subspace as below,
is actually an orthonormal basis of the subspace as below,
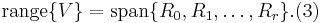
It can be proved that the subspace in~(2) is included in the
subspace in~(3). Due to the numerical stability properties of
the repeated modified Gram-Schmidt process employed in
[2][3], the reduced model derived from 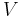 in~(3) is computed in a numerically stable and accurate way.
in~(3) is computed in a numerically stable and accurate way.
![R_0=B_M, \ R_1=[M_1R_0,\ldots, M_pR_0],
R_2=[M_1R_1,\ldots, M_pR_1],
\vdots,
R_r=[M_1R_{r-1},\ldots, M_pR_{r-1}]
\vdots.](/morwiki/images/math/7/f/b/7fbc569d73839ffb50f99bc707354275.png)
