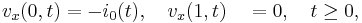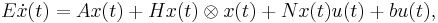Description
The FitzHugh-Nagumo system describes a prototype of an excitable system (e.g., a neuron).
If the external stimulus 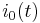 exceeds a certain threshold value, the system will exhibit a characteristic excursion in phase space, before the variables
exceeds a certain threshold value, the system will exhibit a characteristic excursion in phase space, before the variables  and
and 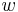 relax back to their rest values. This behaviour is typical for spike generations (=short elevation of membrane voltage
relax back to their rest values. This behaviour is typical for spike generations (=short elevation of membrane voltage  ) in a neuron after stimulation by an external input current.
) in a neuron after stimulation by an external input current.
Here, we present the setting from [1], where the equations for the dynamical system read
with  and initial and boundary conditions
and initial and boundary conditions
where 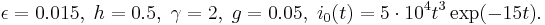 In [1], the previous system of coupled nonlinear PDEs is spatially discretized by means of a finite difference scheme with
In [1], the previous system of coupled nonlinear PDEs is spatially discretized by means of a finite difference scheme with 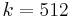 nodes for each PDE. Hence, one obtains a nonlinear (cubic) system of ODEs with state dimension
nodes for each PDE. Hence, one obtains a nonlinear (cubic) system of ODEs with state dimension 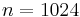 . xx--CrossReference--dft--fig:fhn--xx shows the typical limit cycle behaviour described above.
. xx--CrossReference--dft--fig:fhn--xx shows the typical limit cycle behaviour described above.
Reformulation as a quadratic-bilinear system
Instead of the cubic system of ODEs, one can alternatively study a so-called quadratic-bilinear control system of the form
with 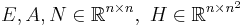 and
and 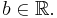 The idea relies on artificially introducing a new state variable defined as
The idea relies on artificially introducing a new state variable defined as 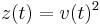 and subsequently computing the dynamics of the new variable, i.e., specifying
and subsequently computing the dynamics of the new variable, i.e., specifying 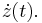 The technique goes back to [2], where it is successfully applied to several smooth nonlinear control-affine systems. As it is discussed in [3], the previously mentioned introduction of
The technique goes back to [2], where it is successfully applied to several smooth nonlinear control-affine systems. As it is discussed in [3], the previously mentioned introduction of 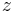 yields a quadratic-bilinear control of dimension
yields a quadratic-bilinear control of dimension 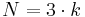 with state vector
with state vector ![x = [v,w,z]^T.](/morwiki/images/math/4/7/4/4741b01381a6996c98ed59a915154932.png) The increase of the state dimension has the advantage of reducing the nonlinearity from cubic to quadratic. This however opens up the possibility to reduce the system by the generalized moment-matching approach from [2], see also [3] for more details on the implementation.
The increase of the state dimension has the advantage of reducing the nonlinearity from cubic to quadratic. This however opens up the possibility to reduce the system by the generalized moment-matching approach from [2], see also [3] for more details on the implementation.
Data
All matrices of the quadratic-bilinear formulation discretized with 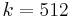 are in the Matrix Market format. The matrix name is used as an extension of the matrix file and can be found at:
are in the Matrix Market format. The matrix name is used as an extension of the matrix file and can be found at:
For the input function, we have ![u(t)=[i_0(t),1]](/morwiki/images/math/b/2/a/b2add9114cf9c4413cc6010d261f2eee.png) . For more information on the discretization details, see [1].
. For more information on the discretization details, see [1].
References
- ↑ 1.0 1.1 1.2 S. Chaturantabut and D.C. Sorensen, "Nonlinear Model Reduction via Discrete Empirical Interpolation", SIAM J. Sci. Comput., 32 (2010), pp. 2737-2764.
- ↑ 2.0 2.1 C. Gu, "QLMOR: A Projection-Based Nonlinear Model Order Reduction Approach Using Quadratic-Linear Representation of Nonlinear Systems", IEEE T. Comput. Aid. D., 30 (2011), pp. 1307-1320.
- ↑ 3.0 3.1 P. Benner and T. Breiten, "Two-sided Moment Matching Methods for Nonlinear Model Eeduction", 2012, Preprint MPIMD/12-12.


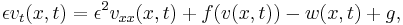
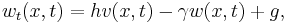
![v(x,0)=0,\quad w(x,0)=0, \quad x\in [0,1],](/morwiki/images/math/a/4/6/a46a8b06dcccd3bdbb094e4acad72a28.png)