| Line 6: | Line 6: | ||
We use the system |
We use the system |
||
| − | <math> |
||
| − | (E_0+s_1 E+s_2E_2+\ldots +s_pE_p)x=Bu(s_1,\ldots,s_p), \quad |
||
| − | y=Cx, \quad \quad \quad \quad (1) |
||
| − | </math> |
||
| − | |||
<math> |
<math> |
||
E \frac{dx(t)}{dt}=A x(t)+B u(t),</math> |
E \frac{dx(t)}{dt}=A x(t)+B u(t),</math> |
||
| Line 16: | Line 11: | ||
y(t)=Cx(t)+Du(t). |
y(t)=Cx(t)+Du(t). |
||
</math> |
</math> |
||
| − | |||
as an example to explain the basic idea. Assuming that an orthonormal |
as an example to explain the basic idea. Assuming that an orthonormal |
||
basis <math>V=(v_1,v_2, \ldots, v_q)</math> of the subspace <math>S_1</math> has been |
basis <math>V=(v_1,v_2, \ldots, v_q)</math> of the subspace <math>S_1</math> has been |
||
| − | found, then the approximation <math>\tilde |
+ | found, then the approximation <math>\tilde x(t)</math> in <math>S_1</math> can be represented by |
| − | the basis as <math>\tilde |
+ | the basis as <math>\tilde x(t)=V z(t)</math>. Therefore <math>x(t)</math> can be approximated by <math> x(t) \approx V z(t)</math>. Here <math>z</math> is a vector |
of length $q \ll n$. |
of length $q \ll n$. |
||
| − | Once <math> |
+ | Once <math>z(t)</math> is computed, we can get an |
| − | approximate solution <math>\tilde |
+ | approximate solution <math>\tilde x(t)=V z(t)</math> for <math>x(t)</math>. The vector <math>z(t)</math> |
can be computed from the reduced model which is derived by the |
can be computed from the reduced model which is derived by the |
||
following two steps. |
following two steps. |
||
Revision as of 16:15, 12 March 2013
The basic idea of almost all the model order reduction (MOR) methods is to
find a subspace 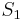 which approximates the manifold where the state
vector Failed to parse (syntax error): {\bf x}(t)
resides. Afterwards, Failed to parse (syntax error): {\bf x}(t)
is approximated by a vector Failed to parse (syntax error): \tilde{\bf x}(t)
in $S_1$. The reduced model is produced by Petrov-Galerkin projection onto a subspace $S_2$, or by Galerkin projection onto the same subspace
which approximates the manifold where the state
vector Failed to parse (syntax error): {\bf x}(t)
resides. Afterwards, Failed to parse (syntax error): {\bf x}(t)
is approximated by a vector Failed to parse (syntax error): \tilde{\bf x}(t)
in $S_1$. The reduced model is produced by Petrov-Galerkin projection onto a subspace $S_2$, or by Galerkin projection onto the same subspace 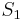 .
.
We use the system
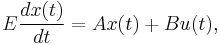
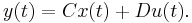 as an example to explain the basic idea. Assuming that an orthonormal
basis
as an example to explain the basic idea. Assuming that an orthonormal
basis 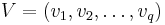 of the subspace
of the subspace 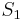 has been
found, then the approximation
has been
found, then the approximation 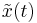 in
in 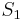 can be represented by
the basis as
can be represented by
the basis as 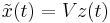 . Therefore
. Therefore 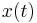 can be approximated by
can be approximated by 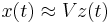 . Here
. Here 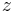 is a vector
of length $q \ll n$.
is a vector
of length $q \ll n$.
Once 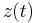 is computed, we can get an
approximate solution
is computed, we can get an
approximate solution 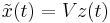 for
for 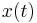 . The vector
. The vector 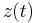 can be computed from the reduced model which is derived by the
following two steps.
can be computed from the reduced model which is derived by the
following two steps.
