| Line 48: | Line 48: | ||
<math> |
<math> |
||
c^{in}_i= |
c^{in}_i= |
||
| − | \begin{array} |
+ | \begin{array}{ll} |
c^F_i, &\text{if $t \le t_{inj}$;}\\ |
c^F_i, &\text{if $t \le t_{inj}$;}\\ |
||
0, &\text{if $t > t_{inj}$.} |
0, &\text{if $t > t_{inj}$.} |
||
Revision as of 11:41, 20 November 2012
Description of physical model
Preparative liquid chromatography as a crucial separation and purification tool has been widely employed in food, fine chemical and pharmaceutical industries. Chromatographic separation at industry scale can be operated either discontinuously or in a continuous mode. The continuous case will be addressed in the benchmark SMB, and here we focus on the discontinuous mode -- batch chromatography.
The principle of batch elution chromatography for the binary separation is shown schematically in Fig.1 below. During the injection period
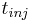 , a mixture consisting of A and B is injected at the inlet of the column packed with a suitable stationary phase.
With the help of the mobile phase, the feed mixture then flows through the column. Since the solutes to be separated exhibit different
adsorption affinities to the stationary phase, they move at different velocities in the column, and thus separate from each other
when exiting the column. At the column outlet, component A is collected between cutting points
, a mixture consisting of A and B is injected at the inlet of the column packed with a suitable stationary phase.
With the help of the mobile phase, the feed mixture then flows through the column. Since the solutes to be separated exhibit different
adsorption affinities to the stationary phase, they move at different velocities in the column, and thus separate from each other
when exiting the column. At the column outlet, component A is collected between cutting points 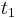 and
and 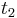 ,
and component B is collected between
,
and component B is collected between 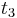 and
and 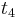 . Here the positions of
. Here the positions of 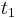 and
and 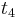 are determined by a minimum concentration threshold that the detector can resolve. The positions of
are determined by a minimum concentration threshold that the detector can resolve. The positions of 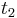 and
and 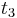 are determined by the purity specifications imposed on the products. After the cycle period
are determined by the purity specifications imposed on the products. After the cycle period 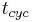 , the injection is repeated.
The feed flow-rate
, the injection is repeated.
The feed flow-rate  and injection period
and injection period 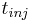 are often considered as the operating variables.
By properly choosing them, the process can achieve the desired performance criterion, such as production rate, while respecting
the product specifications (e.g., purity, recovery yield).
are often considered as the operating variables.
By properly choosing them, the process can achieve the desired performance criterion, such as production rate, while respecting
the product specifications (e.g., purity, recovery yield).
The batch chromatography can be described as the following convection-diffusion system,
![\frac{\partial c_i}{\partial t}+\frac{1-\epsilon}{\epsilon}\frac{\partial q_i}{\partial t}+u\frac{\partial c_i}{\partial z}-D_i\frac{\partial^2 c_i}{\partial z^2}=0,
\qquad \qquad [1]](/morwiki/images/math/2/4/e/24e06951c233d375b35c7242e8516874.png)
![\frac{\partial q_i}{\partial t} = K_{m,i}\,(q^{Eq}_i-q_i), \qquad z\in (0,\;L), \qquad \qquad [2]](/morwiki/images/math/a/c/d/acd8ccdb3641e5405c0de4ff8d9be150.png)
where 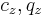 are concentrations of component
are concentrations of component 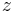 in the liquid
and solid phase, and
in the liquid
and solid phase, and 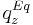 is the adsorption equilibrium concentration defined as
is the adsorption equilibrium concentration defined as
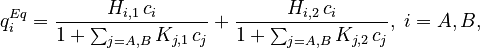
The boundary conditions for Eq. [1] are specified by the Danckwerts relations:
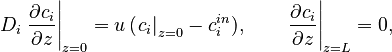 where
where 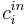 is the concentration of component
is the concentration of component  at the inlet of the column. A rectangular injection is assumed for the system and thus
Failed to parse (lexing error): c^{in}_i= \begin{array}{ll} c^F_i, &\text{if $t \le t_{inj}$;}\\ 0, &\text{if $t > t_{inj}$.} \end{array} <math> where <math>c^F_i<math> is the feed concentration for component <math>i
and
at the inlet of the column. A rectangular injection is assumed for the system and thus
Failed to parse (lexing error): c^{in}_i= \begin{array}{ll} c^F_i, &\text{if $t \le t_{inj}$;}\\ 0, &\text{if $t > t_{inj}$.} \end{array} <math> where <math>c^F_i<math> is the feed concentration for component <math>i
and 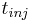 is the injection period. In addition, the column is assumed unloaded initially:
is the injection period. In addition, the column is assumed unloaded initially:
![c_i(t=0,z)=q_i(t=0,z)=0,\quad z\in[0,\;L],\;i=A,B.](/morwiki/images/math/b/0/a/b0aa2a0c8998935c2a0c5700b09d7887.png)
