Difference between revisions of "MESS"

Revision as of 18:41, 15 November 2012

MESS, the Matrix Equations and Sparse Solvers library, is the successor to the Lyapack Toolbox for MATLAB. It will be available as a MATLAB toolbox, as well as, a C-library. It is intended for solving large sparse matrix equations as well as problems from model order reduction and optimal control. The C version provides a large set of axillary subroutines for sparse matrix computations and efficient usage of modern multicore workstations.

A list of the main features (some prtially finished at the current stage) of both the MATLAB and C versions is:

Solvers for large and sparse matrix Riccati (algebraic and differential) and Lyapunov (algebraic) equations
Balanced Truncation based MOR for first and second order state space systems and index 1 DAEs
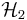$\mathcal{H}_2$ -MOR via the IRKA and TSIA algorithms
Basic tools for Large sparse linear quadratic optimal control problems

The C version moreover provides:

sophisticated Multicore parallelism
compressed file I/O
uniform access to linear algebra routines
specially structured Sylvester equation solvers
interfaces to BLAS, LAPACK, Suitesparse, Slicot

Contact information:
Jens Saak

@@ Line 8: / Line 8: @@
 * Solvers for large and sparse matrix Riccati (algebraic and differential) and Lyapunov (algebraic) equations
 * Balanced Truncation based MOR for first and second order state space systems and index 1 DAEs
-* <math>\mathcal{H}_2</math> MOR via the IRKA and TSIA algorithms
+* <math>\mathcal{H}_2</math>-MOR via the IRKA and TSIA algorithms
 * Basic tools for Large sparse linear quadratic optimal control problems