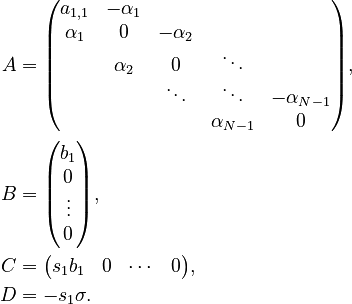(Fixes, Python code, N->n) |
(Edit categories, replace source tags) |
||
| Line 2: | Line 2: | ||
[[Category:procedural]] |
[[Category:procedural]] |
||
[[Category:linear]] |
[[Category:linear]] |
||
| ⚫ | |||
[[Category:time invariant]] |
[[Category:time invariant]] |
||
| ⚫ | |||
| + | [[Category:Sparse]] |
||
[[Category:SISO]] |
[[Category:SISO]] |
||
| Line 49: | Line 50: | ||
<!-- TODO add unbalancing transformation --> |
<!-- TODO add unbalancing transformation --> |
||
| − | :< |
+ | :<syntaxhighlight lang="matlab"> |
function [A,B,C,D] = allpass(n) |
function [A,B,C,D] = allpass(n) |
||
% allpass (all-pass system) |
% allpass (all-pass system) |
||
| Line 62: | Line 63: | ||
D = 1; |
D = 1; |
||
end |
end |
||
| + | </syntaxhighlight> |
||
| − | </source> |
||
The function call requires one argument; the number of states <math>n</math>. |
The function call requires one argument; the number of states <math>n</math>. |
||
The return value consists of four matrices; the system matrix <math>A</math>, the input matrix <math>B</math>, the output matrix <math>C</math>, and the feed-through matrix <math>D</math>. |
The return value consists of four matrices; the system matrix <math>A</math>, the input matrix <math>B</math>, the output matrix <math>C</math>, and the feed-through matrix <math>D</math>. |
||
| − | :< |
+ | :<syntaxhighlight lang="matlab"> |
[A,B,C,D] = allpass(n); |
[A,B,C,D] = allpass(n); |
||
| + | </syntaxhighlight> |
||
| − | </source> |
||
An equivalent [https://www.python.org/ Python] code is |
An equivalent [https://www.python.org/ Python] code is |
||
| − | :< |
+ | :<syntaxhighlight lang="python"> |
from scipy.sparse import diags, lil_matrix |
from scipy.sparse import diags, lil_matrix |
||
| Line 86: | Line 87: | ||
D = 1 |
D = 1 |
||
return A, B, C, D |
return A, B, C, D |
||
| + | </syntaxhighlight> |
||
| − | </source> |
||
==Dimensions== |
==Dimensions== |
||
Revision as of 17:38, 29 August 2023
Description
This procedural benchmark generates an all-pass SISO system based on [1].
For an all-pass system, the transfer function has the property 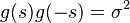 ,
, 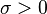 ,
or (equivalently) the controllability and observability Gramians are quasi inverse to each other:
,
or (equivalently) the controllability and observability Gramians are quasi inverse to each other: 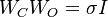 ,
which means this system has a single Hankel singular value of multiplicity of the system's order.
The system matrices are constructed based on the scheme:
,
which means this system has a single Hankel singular value of multiplicity of the system's order.
The system matrices are constructed based on the scheme:
We choose 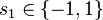 to be
to be 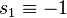 , as this makes the system state-space-anti-symmetric.
Furthermore,
, as this makes the system state-space-anti-symmetric.
Furthermore, 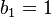 and
and 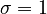 , which makes
, which makes 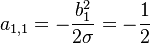 .
.
Data
This benchmark is procedural and the state dimensions can be chosen. Use the following MATLAB code to generate a random system as described above:
function [A,B,C,D] = allpass(n) % allpass (all-pass system) % by Christian Himpe, 2020 % released under BSD 2-Clause License %* A = gallery('tridiag',n,-1,0,1); A(1,1) = -0.5; B = sparse(1,1,1,n,1); C = -B'; D = 1; end
The function call requires one argument; the number of states  .
The return value consists of four matrices; the system matrix
.
The return value consists of four matrices; the system matrix  , the input matrix
, the input matrix  , the output matrix
, the output matrix  , and the feed-through matrix
, and the feed-through matrix 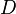 .
.
[A,B,C,D] = allpass(n);
An equivalent Python code is
from scipy.sparse import diags, lil_matrix def allpass(n): A = diags([-1, 0, 1], offsets=[-1, 0, 1], shape=(n, n), format='lil') A[0, 0] = -0.5 A = A.tocsc() B = lil_matrix((n, 1)) B[0, 0] = 1 B = B.tocsc() C = -B.T D = 1 return A, B, C, D
Dimensions
System dimensions:
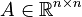 ,
,
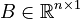 ,
,
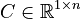 ,
,
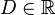 .
.
Citation
To cite this benchmark, use the following references:
- For the benchmark itself and its data:
- The MORwiki Community, All-Pass System. MORwiki - Model Order Reduction Wiki, 2020. http://modelreduction.org/index.php/All_pass_system
@MISC{morwiki_allpass,
author = {{The MORwiki Community}},
title = {All-Pass System},
howpublished = {{MORwiki} -- Model Order Reduction Wiki},
url = {http://modelreduction.org/index.php/All_pass_system},
year = {2020}
}
References
- ↑ R.J. Ober. "Asymptotically Stable All-Pass Transfer Functions: Canonical Form, Parametrization and Realization", IFAC Proceedings Volumes, 20(5): 181--185, 1987.