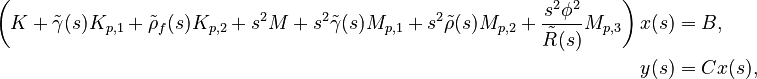| Line 18: | Line 18: | ||
:<math> |
:<math> |
||
\begin{align} |
\begin{align} |
||
| − | \left( |
+ | \left( K + \tilde{\gamma}(s) K_{p,1} + \tilde{\rho}_f(s) K_{p,2} + s^2 M + s^2 \tilde{\gamma}(s) M_{p,1} + s^2 \tilde{\rho}(s) M_{p,2} + \frac{s^2 \phi^2}{\tilde{R}(s)} M_{p,3} \right) x(s) &= B, \\ |
y(s) &= C x(s), |
y(s) &= C x(s), |
||
\end{align} |
\end{align} |
||
| Line 27: | Line 27: | ||
System dimensions: |
System dimensions: |
||
| − | <math> |
+ | <math>K, K_{p,1}, K_{p,2}, M, M_{p,1}, M_{p,2}, M_{p,3} \in \mathbb{R}^{n \times n}</math>, |
<math>B \in \mathbb{R}^{n \times 1}</math>, |
<math>B \in \mathbb{R}^{n \times 1}</math>, |
||
<math>C \in \mathbb{R}^{1 \times n}</math>, |
<math>C \in \mathbb{R}^{1 \times n}</math>, |
||
Revision as of 16:25, 27 June 2023
 Note: This page has not been verified by our editors.
Note: This page has not been verified by our editors.
Description
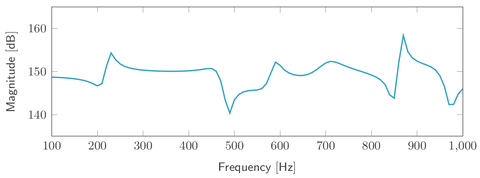
The Porous absorber benchmark models the sound pressure in a cavity excited by a single harmonic load. One side of the cavity is covered by a layer of poroelastic material, which adds dissipation to the system. The geometry of this model follows [1]. Various projection-based model order reduction methods have been applied and compared using this example as a benchmark in [2].
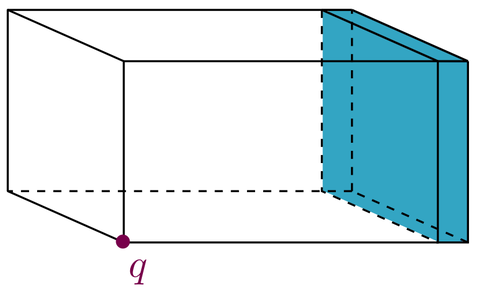
The cavity has the dimensions 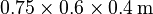 and one wall is covered by a
and one wall is covered by a 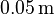 thick poroelastic layer acting as a sound absorber. The poroelastic material is described by the Biot theory[3] and the system is excited by a point source located in a corner opposite of the porous layer. The material parameters for the acoustic fluid and the poroelastic material have been chosen according to[1].
thick poroelastic layer acting as a sound absorber. The poroelastic material is described by the Biot theory[3] and the system is excited by a point source located in a corner opposite of the porous layer. The material parameters for the acoustic fluid and the poroelastic material have been chosen according to[1].
Dimensions
System structure:
with the frequency dependent functions for the effective densities 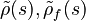 , the parameter
, the parameter 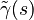 relating the effective densities and the frequency dependent elasticity coefficients to the porosity, and the scaled effective bulk modulus
relating the effective densities and the frequency dependent elasticity coefficients to the porosity, and the scaled effective bulk modulus 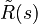 . For more details on the functions, see [1].
. For more details on the functions, see [1].
System dimensions:
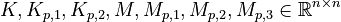 ,
,
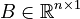 ,
,
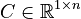 ,
with
,
with 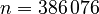 .
.
Data
The data is available at Zenodo.
References
- ↑ 1.0 1.1 1.2 R. Rumpler, P. Göransson, J.-F. Deü. "A finite element approach combining a reduced-order system, Padé approximants, and an adaptive frequency windowing for fast multi-frequency solution of poro-acoustic problems", International Journal for Numerical Methods in Engineering, 97: 759-784, 2014.
- ↑ Q. Aumann, S. W. R. Werner. "Structured model order reduction for vibro-acoustic problems using interpolation and balancing methods", Journal of Sound and Vibration, 543: 117363, 2023.
- ↑ M. A. Biot. "Theory of propagation of elastic waves in a fluid-saturated porous solid. I. Low-frequency range", J. Acoust. Soc. Am., 28(2):168–178, 1956.

 .
.