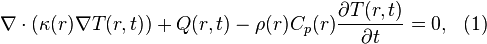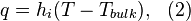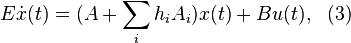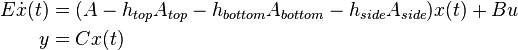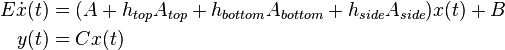(→Data) |
m |
||
| Line 174: | Line 174: | ||
<ref name="feng2004">L. Feng, E.B. Rudnyi, J.G. Korvink, "<span class="plainlinks">[http://modelreduction.com/doc/papers/feng04THERMINIC.pdf Parametric Model Reduction to Generate Boundary Condition Independent Compact Thermal Model]</span>", THERMINIC 2004, 10th International Workshop on Thermal Investigations of ICs and Systems, 29 September - 1 October 2004, Sophia Antipolis, Cote d'Azur, France.</ref> |
<ref name="feng2004">L. Feng, E.B. Rudnyi, J.G. Korvink, "<span class="plainlinks">[http://modelreduction.com/doc/papers/feng04THERMINIC.pdf Parametric Model Reduction to Generate Boundary Condition Independent Compact Thermal Model]</span>", THERMINIC 2004, 10th International Workshop on Thermal Investigations of ICs and Systems, 29 September - 1 October 2004, Sophia Antipolis, Cote d'Azur, France.</ref> |
||
| − | <ref name="feng2005">L. Feng, E. B. Rudnyi, J. G. Korvink, "<span class="plainlinks">[10.1109/TCAD.2005.852660 Preserving the film coefficient as a parameter in the compact thermal model for fast electro-thermal simulation]</span>", IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 24(12): 1838--1847, 2005.</ref> |
+ | <ref name="feng2005">L. Feng, E. B. Rudnyi, J. G. Korvink, "<span class="plainlinks">[https://doi.org/10.1109/TCAD.2005.852660 Preserving the film coefficient as a parameter in the compact thermal model for fast electro-thermal simulation]</span>", IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 24(12): 1838--1847, 2005.</ref> |
<ref name="korvink2005"> J.G. Korvink, E.B. Rudnyi, <span class="plainlinks">[https://doi.org/10.1007/3-540-27909-1_11 Oberwolfach Benchmark Collection]</span>, Dimension Reduction of Large-Scale Systems, Lecture Notes in Computational Science and Engineering, vol 45: 311--315, 2005.</ref> |
<ref name="korvink2005"> J.G. Korvink, E.B. Rudnyi, <span class="plainlinks">[https://doi.org/10.1007/3-540-27909-1_11 Oberwolfach Benchmark Collection]</span>, Dimension Reduction of Large-Scale Systems, Lecture Notes in Computational Science and Engineering, vol 45: 311--315, 2005.</ref> |
||
Revision as of 16:48, 26 January 2022
Description: Boundary Condition Independent Thermal Model
A benchmark for the heat transfer problem with variable film coefficients is presented. It can be used to apply parametric model reduction algorithms to a linear first-order problem.
Modeling
An important requirements for a compact thermal model is that it should be independent from the boundary condition. This means that a chip producer does not know conditions under which the chip will be used and hence the chip compact thermal model must allow an engineer to research on how the change in the environment influences the chip temperature. The chip benchmarks representing boundary condition independent requirements are described in [1].
Let us briefly describe the mathematical problem. The thermal problem can be modeled by the heat transfer partial differential equation
with  is the position,
is the position, 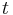 is the time,
is the time,  is the thermal conductivity of the material,
is the thermal conductivity of the material, 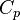 is the specific heat capacity,
is the specific heat capacity,  is the mass density,
is the mass density,  is the heat generation rate, and
is the heat generation rate, and  is the unknown temperature distribution to be determined.
The heat exchange through device interfaces is usually modeled by convection boundary conditions
is the unknown temperature distribution to be determined.
The heat exchange through device interfaces is usually modeled by convection boundary conditions
where  is the heat flow through a given point,
is the heat flow through a given point, 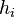 is the film coefficient to describe the heat exchange for the
is the film coefficient to describe the heat exchange for the  -th interface,
-th interface,  is the local temperature at this point, and
is the local temperature at this point, and 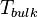 is the bulk temperature in the neighboring phase (in most cases
is the bulk temperature in the neighboring phase (in most cases 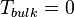 ).
).
After the discretization of equations (1) and (2) one obtains a system of ordinary differential equations as follows
where  and
and  are the device system matrices,
are the device system matrices,  is the diagonal matrix due to the discretization of equation (2) for the
is the diagonal matrix due to the discretization of equation (2) for the  -th interface,
-th interface, 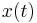 is the vector with unknown temperatures.
is the vector with unknown temperatures.
In terms of the equation (3) above, the engineering requirements read as follows.
A chip producer specifies the system matrices but the film coefficient, 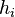 , is controlled later on by another engineer.
As such, any reduced model to be useful should preserve
, is controlled later on by another engineer.
As such, any reduced model to be useful should preserve 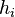 in the symbolic form.
This problem can be mathematically expressed as parametric model reduction[2][3][4].
in the symbolic form.
This problem can be mathematically expressed as parametric model reduction[2][3][4].
Unfortunately, the benchmark from [1] is not available in the computer readable format.
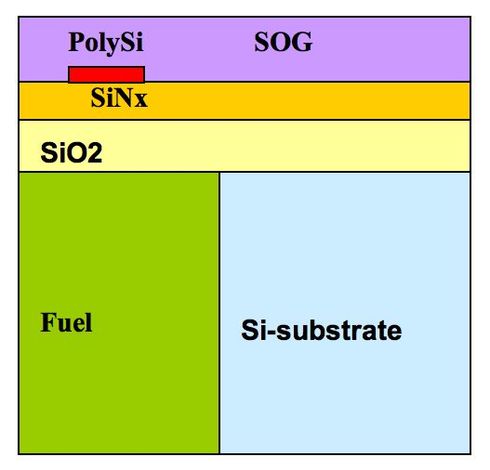
For research purposes, we have modified a Micropyros Thruster benchmark (see Fig. 1).
In the context of the present work, the model is as a generic example of a device with a single heat source when the generated heat dissipates through the device to the surroundings. The exchange between surrounding and the device is modeled by convection boundary conditions with different film coefficients at the top, 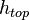 , bottom,
, bottom, 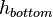 , and the side,
, and the side, 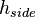 .
From this viewpoint, it is quite similar to a chip model used as a benchmark in [1].
The goal of parametric model reduction in this case is to preserve
.
From this viewpoint, it is quite similar to a chip model used as a benchmark in [1].
The goal of parametric model reduction in this case is to preserve 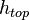 ,
, 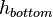 , and
, and 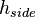 in the reduced model in the symbolic form.
in the reduced model in the symbolic form.
Discretization
We have used a 2D-axisymmetric microthruster model (T2DAL in Micropyros Thruster).
The model has been made in ANSYS and system matrices have been extracted by means of mor4fem [5].
The benchmark contains a constant load vector.
The input function equal to one corresponds to the constant input power of  .
.
The linear ordinary differential equations of first order are written as:
where  and
and  are the symmetric sparse system matrices (heat capacity and heat conductivity matrix),
are the symmetric sparse system matrices (heat capacity and heat conductivity matrix),  is the load vector,
is the load vector,  is the output matrix,
is the output matrix, 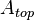 ,
, 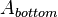 , and
, and 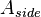 are the diagonal matrices from the discretization of the convection boundary conditions and
are the diagonal matrices from the discretization of the convection boundary conditions and  is the vector of unknown temperatures.
is the vector of unknown temperatures.
The numerical values of film coefficients, 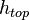 ,
, 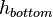 , and
, and 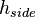 can be from
can be from 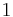 to
to  .
Typical important sets film coefficients can be found in [1].
The allowable approximation error is
.
Typical important sets film coefficients can be found in [1].
The allowable approximation error is 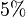 [1].
[1].
The benchmark has been used in [6][7] where the problem is also described in more detail.
Acknowledgements
This work was partially funded by the DFG project MST-Compact (KO-1883/6), the Italian research council CNR together with the Italian province of Trento PAT, by the German Ministry of Research BMBF (SIMOD), and an operating grant of the University of Freiburg.
Origin
This benchmark is part of the Oberwolfach Benchmark Collection[8]; No. 38865, see [9].
Data
The matrices of this benchmark can be downloaded in the Matrix Market format:
- ThermalModel-dim1e3-T2DAL_BCI.tar.gz, 218.7 kB.
The matrix name is used as an extension of the matrix file. File T2DAL_BCI.C.names contains a list of output names written consecutively.
Dimensions
System structure:
System dimensions:
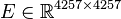 ,
,
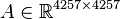 ,
,
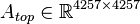 ,
,
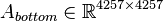 ,
,
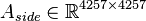 ,
,
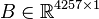 ,
,
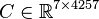 .
.
Parameter ranges:
![h_{top} \in [1,10^9]](/morwiki/images/math/c/b/c/cbc61083d41617bf32341d786f5c82cf.png) ,
,
![h_{bottom} \in [1,10^9]](/morwiki/images/math/3/f/b/3fbb51c224b5eb2e895e7970074da222.png) ,
,
![h_{side} \in [1,10^9]](/morwiki/images/math/a/6/1/a61849f13df41926ba047f0ba997a86c.png) .
.
Citation
To cite this benchmark, use the following references:
- For the benchmark itself and its data:
- Oberwolfach Benchmark Collection, Thermal Model. hosted at MORwiki - Model Order Reduction Wiki, 2018. http://modelreduction.org/index.php/Thermal_Model
@MISC{morwiki_thermal,
author = {{Oberwolfach Benchmark Collection}},
title = {Thermal Model},
howpublished = {hosted at {MORwiki} -- Model Order Reduction Wiki},
url = {http://modelreduction.org/index.php/Thermal_Model},
year = 20XX
}
- For the background on the benchmark:
@TechReport{morFenRK04,
author = {Feng, L. and Rudnyi, E.~B. and Korvink, J.~G.},
title = {Parametric Model Reduction to Generate Boundary Condition Independent Compact Thermal Model},
institution = {IMTEK-Institute for Microsystem Technology},
type = {Technical report},
year = {2004},
url = {http://modelreduction.com/doc/papers/feng04THERMINIC.pdf}
}
References
- ↑ 1.0 1.1 1.2 1.3 1.4 C.J.M. Lasance, "Two benchmarks to facilitate the study of compact thermal modeling phenomena", IEEE Transactions on Components and Packaging Technologies, 24: 559--565, 2001.
- ↑ D.S. Weile, E. Michielssen, E. Grimme, K. Gallivan, "A method for generating rational interpolant reduced order models of two-parameter linear systems", Applied Mathematics Letters, 12: 93--102, 1999.
- ↑ P. K. Gunupudi, R. Khazaka, M. S. Nakhla, T. Smy, and D. Celo, "Passive parameterized time-domain macromodels for high-speed transmission-line networks", IEEE Transactions on Microwave Theory and Techniques, 51: 2347--2354, 2003.
- ↑ L. Daniel, O.C. Siong, L.S. Chay, K.H. Lee, and J. White, "A Multiparameter Moment-Matching Model-Reduction Approach for Generating Geometrically Parameterized Interconnect Performance Models", IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 23: 678--693, 2004.
- ↑ E.B. Rudnyi and J.G. Korvink, "Model Order Reduction of MEMS for Efficient Computer Aided Design and System Simulation", MTNS2004, Sixteenth International Symposium on Mathematical Theory of Networks and Systems, Katholieke Universiteit Leuven, Belgium, July 5-9, 2004.
- ↑ L. Feng, E.B. Rudnyi, J.G. Korvink, "Parametric Model Reduction to Generate Boundary Condition Independent Compact Thermal Model", THERMINIC 2004, 10th International Workshop on Thermal Investigations of ICs and Systems, 29 September - 1 October 2004, Sophia Antipolis, Cote d'Azur, France.
- ↑ L. Feng, E. B. Rudnyi, J. G. Korvink, "Preserving the film coefficient as a parameter in the compact thermal model for fast electro-thermal simulation", IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 24(12): 1838--1847, 2005.
- ↑ J.G. Korvink, E.B. Rudnyi, Oberwolfach Benchmark Collection, Dimension Reduction of Large-Scale Systems, Lecture Notes in Computational Science and Engineering, vol 45: 311--315, 2005.
- ↑ E.B. Rudnyi, J.G. Korvink, Boundary Condition Independent Thermal Model, Dimension Reduction of Large-Scale Systems, Lecture Notes in Computational Science and Engineering, vol 45: 345--348, 2005.