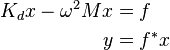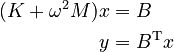(Minor fixes.) |
(Fix CrossRefs) |
||
| Line 39: | Line 39: | ||
\{0.5j,j=1,\ldots,m\}</math> with <math>m=400</math>. |
\{0.5j,j=1,\ldots,m\}</math> with <math>m=400</math>. |
||
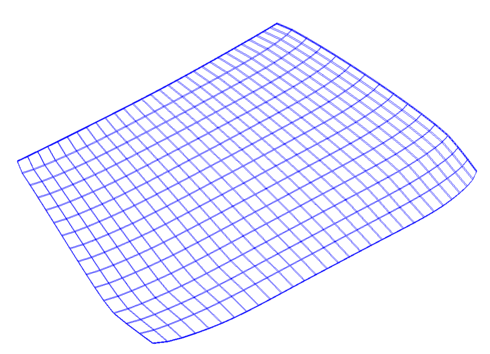
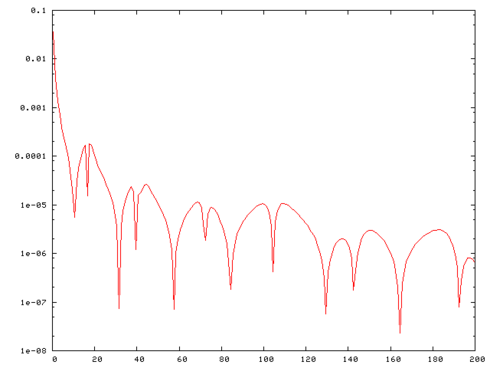
| − | + | Fig. 1 shows the mesh of the car windscreen and Fig. 2 the frequency response <math>\vert \Re(y(\omega)) \vert</math>. |
|
==Origin== |
==Origin== |
||
Revision as of 08:53, 27 August 2021
Description
This is an example for a model in the frequency domain of the form
where 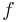 represents a unit point load in one unknown of the state vector.
represents a unit point load in one unknown of the state vector.
 is a symmetric positive-definite matrix and
is a symmetric positive-definite matrix and 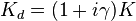 where
where 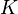 is symmetric positive semi-definite.
is symmetric positive semi-definite.
The test problem is a structural model of a car windscreen. [1]
This is a 3D problem discretized with 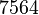 nodes and
nodes and 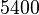 linear hexahedral elements (3 layers of
linear hexahedral elements (3 layers of 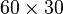 elements).
The mesh is shown in xx--CrossReference--dft--fig1--xx.
The material is glass with the following properties:
The Young modulus is
elements).
The mesh is shown in xx--CrossReference--dft--fig1--xx.
The material is glass with the following properties:
The Young modulus is 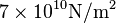 , the density is
, the density is 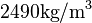 , and the Poisson ratio is
, and the Poisson ratio is 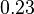 . The natural damping is
. The natural damping is 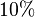 , i.e.
, i.e. 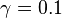 .
The structural boundaries are free (free-free boundary conditions).
The windscreen is subjected to a point force applied on a corner.
The goal of the model reduction is the fast evaluation of
.
The structural boundaries are free (free-free boundary conditions).
The windscreen is subjected to a point force applied on a corner.
The goal of the model reduction is the fast evaluation of 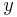 .
Model reduction is used as a fast linear solver for a sequence of parametrized linear systems.
.
Model reduction is used as a fast linear solver for a sequence of parametrized linear systems.
The discretized problem has dimension 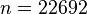 .
The goal is to estimate
.
The goal is to estimate 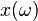 for
for ![\omega\in[0.5,200]](/morwiki/images/math/b/b/0/bb02974887d08c7449464802fbf5ea4c.png) .
In order to generate the plots, the frequency range was discretized as
.
In order to generate the plots, the frequency range was discretized as  with
with 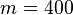 .
.
Fig. 1 shows the mesh of the car windscreen and Fig. 2 the frequency response 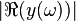 .
.
Origin
This benchmark is part of the Oberwolfach Benchmark Collection[2]; No. 38886.
Data
Download matrices in the Matrix Market format:
- Windscreen-dim1e4-windscreen.tar.gz (21.5 MB)
The archive contains files windscreen.K, windscreen.M and windscreen.B representing 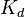 ,
, 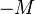 and
and 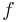 accordingly.
accordingly.
Dimensions
System structure:
with ![\omega \in [0.5, 200]](/morwiki/images/math/b/b/0/bb02974887d08c7449464802fbf5ea4c.png) .
.
System dimensions:
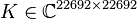 ,
,
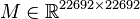 ,
,
 .
.
Citation
To cite this benchmark, use the following references:
- For the benchmark itself and its data:
- Oberwolfach Benchmark Collection, Windscreen. hosted at MORwiki - Model Order Reduction Wiki, 2018. http://modelreduction.org/index.php/Windscreen
@MISC{morwiki_windscreen,
author = {{Oberwolfach Benchmark Collection}},
title = {Windscreen},
howpublished = {hosted at {MORwiki} -- Model Order Reduction Wiki},
url = {http://modelreduction.org/index.php/Windscreen},
year = 20XX
}
- For the background on the benchmark:
@article{Mee07,
author = {K. Meerbergen},
title = {Fast frequency response computation for {R}ayleigh damping},
journal = {International Journal for Numerical Methods in Engineering},
volume = {73},
number = {1},
pages = {96--106},
year = {2007},
doi = {10.1002/nme.2058},
}
References
- ↑ K. Meerbergen, Fast frequency response computation for Rayleigh damping, International Journal for Numerical Methods in Engineering, 73(1): 96--106, 2007.
- ↑ J.G. Korvink, E.B. Rudnyi, Oberwolfach Benchmark Collection, In: Dimension Reduction of Large-Scale Systems, Lecture Notes in Computational Science and Engineering, vol 45: 311--315, 2005.