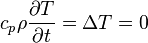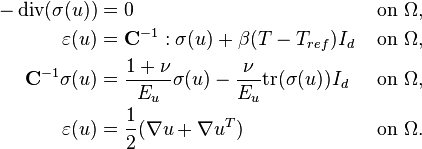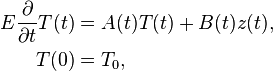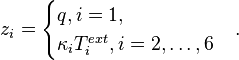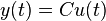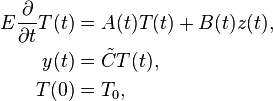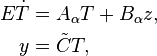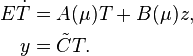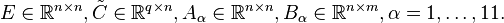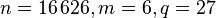| Line 68: | Line 68: | ||
:<math> |
:<math> |
||
z_i=\begin{cases} |
z_i=\begin{cases} |
||
| − | + | q, i=1,\\ |
|
\kappa_i T_i^{ext}, i=2,\dots,6 |
\kappa_i T_i^{ext}, i=2,\dots,6 |
||
\end{cases}. |
\end{cases}. |
||
Revision as of 10:32, 16 August 2018
1 Description
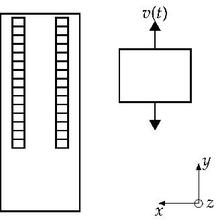
The vertical stand (see xx--CrossReference--dft--fig:cad--xx) represents a structural part of a machine tool. On one of its surfaces a pair of guide rails is located. Caused by a machining process a tool slide is moving on these rails. The machining process produces a certain amount of heat which is transported through the structure into the vertical stand. This heat source is considered to be a temperature input at the guide rails. The induced temperature field, denoted by  is modeled by the heat equation
is modeled by the heat equation
with the boundary conditions
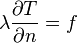 on
on 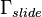 (surface where the tool slide is moving on the guide rails),
(surface where the tool slide is moving on the guide rails),
describing the heat transfer between the tool slide and the vertical stand. The heat transfer to the ambiance is given by the fixed Robin-type boundary condition
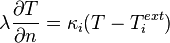 on
on 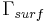 (remaining boundaries).
(remaining boundaries).
The motion driven temperature input and the associated change in the temperature field  lead to deformations
lead to deformations  within the stand structure. Further, it is assumed that no external forces are induced to the system such that the deformation is purely driven by the change of temperature. Since the mechanical behavior of the machine stand is assumed to be much faster than the propagation of the thermal field, it is sufficient to consider the stationary linear elasticity equations
within the stand structure. Further, it is assumed that no external forces are induced to the system such that the deformation is purely driven by the change of temperature. Since the mechanical behavior of the machine stand is assumed to be much faster than the propagation of the thermal field, it is sufficient to consider the stationary linear elasticity equations
Geometrical dimensions:
Stand: Width ( direction):
direction): 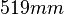 , Height (
, Height (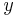 direction):
direction): 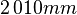 , Depth (
, Depth ( direction):
direction): 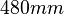
Guide rails: ![y\in [519, 2\,004] mm](/morwiki/images/math/d/6/6/d6623742beb91c8320ac3a3a6356fe02.png)
Slide: Width: 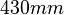 , Height:
, Height: 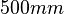 , Depth:
, Depth: 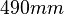
1.1 Discretized Model
The solid model has been generated and meshed in ANSYS. For the spatial discretization the finite element method with linear Lagrange elements has been used and is implemented in FEniCS. The resulting system of ordinary differential equations (ODE), representing the thermal behavior of the stand, reads
with  and a system dimension of
and a system dimension of 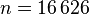 degrees of freedom and
degrees of freedom and 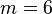 inputs. Note that
inputs. Note that 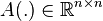 and
and 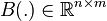 are time-dependent matrix-valued functions. That is, the underlying model is represented by a linear time-Varying (LTV) state-space system. More precisely, here the time dependence originates from the change of the boundary condition on
are time-dependent matrix-valued functions. That is, the underlying model is represented by a linear time-Varying (LTV) state-space system. More precisely, here the time dependence originates from the change of the boundary condition on 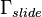 due to the motion of the tool slide. The system input is, according to the boundary conditions, given by
due to the motion of the tool slide. The system input is, according to the boundary conditions, given by
The discretized stationary elasticity model becomes
For the observation of the displacements in single points/regions of interest an output equation of the form
is given.
Exploiting the one-sided coupling of the temperature and deformation fields, and reorganizing the elasticity equation in the form 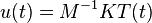 , the heat equation and the elasticity model can easily be combined via the output equation. Finally, the thermo-elastic control system is of the form
, the heat equation and the elasticity model can easily be combined via the output equation. Finally, the thermo-elastic control system is of the form
where the modified output matrix 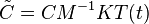 includes the entire elasticity information.
includes the entire elasticity information.
The motion of the tool slide and the associated variation of the affected input boundary are modeled by two different system representations. The following specific model representations have been developed and investigated in [1], [2].
1.2 Switched Linear System
For the model description as a switched linear system, the guide rails of the machine stand are modeled as fifteen equally distributed horizontal segments with a height of 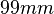 (see a schematic depiction in xx--CrossReference--dft--fig:segm--xx). Any of these segments is assumed to be completely covered by the tool slide if its midpoint (in y-direction) lies within the height of the slide. On the other hand, each segment whose midpoint is not covered is treated as not in contact and therefore the slide always covers five to six segments at each time. Still, the covering of six segments does not have a significant effect on the behavior of the temperature and displacement fields. Due to that and in order to keep the number of subsystems small, this scenario will be neglected. Than, in fact eleven distinct, discrete boundary condition configurations for the stand model that are prescribed by the geometrical dimensions of the segmentation and the tool slide are defined. These distinguishable setups define the subsystems
(see a schematic depiction in xx--CrossReference--dft--fig:segm--xx). Any of these segments is assumed to be completely covered by the tool slide if its midpoint (in y-direction) lies within the height of the slide. On the other hand, each segment whose midpoint is not covered is treated as not in contact and therefore the slide always covers five to six segments at each time. Still, the covering of six segments does not have a significant effect on the behavior of the temperature and displacement fields. Due to that and in order to keep the number of subsystems small, this scenario will be neglected. Than, in fact eleven distinct, discrete boundary condition configurations for the stand model that are prescribed by the geometrical dimensions of the segmentation and the tool slide are defined. These distinguishable setups define the subsystems
of the switched linear system [3], where 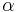 is a piecewise constant function of time, which takes its value from the index set
is a piecewise constant function of time, which takes its value from the index set 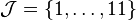 . To be more precise, the switching signal
. To be more precise, the switching signal  implicitly maps the slide position to the number of the currently active subsystem.
implicitly maps the slide position to the number of the currently active subsystem.
1.3 Linear Parameter-Varying System
For the parametric model description, the FE nodes located at the guide rails are clustered with respect to their y-coordinates. This results in 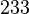 distinct layers in y-direction. According to these layers, the matrices
distinct layers in y-direction. According to these layers, the matrices 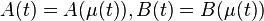 are defined in a parameter-affine representation of the form
are defined in a parameter-affine representation of the form
with the scalar functions 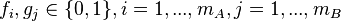 selecting the active layers, covered by the tool slide. The matrix
selecting the active layers, covered by the tool slide. The matrix 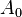 represents the discretization of the Laplacian
represents the discretization of the Laplacian 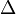 , as well as the discrete portions of
, as well as the discrete portions of 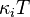 from the Robin-type boundaries, associated to the exchange with the ambience given by the inputs
from the Robin-type boundaries, associated to the exchange with the ambience given by the inputs 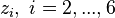 . The remaining summands
. The remaining summands 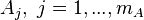 denote the discretization of
denote the discretization of 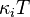 from the moving Robin-type boundaries.
from the moving Robin-type boundaries.
Note that in general the number of summands of these representations need not to be equal. Still, according to the number of layers, for this example, it holds 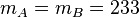 . For more details on parametric models, see e.g., [4] and the references therein.
. For more details on parametric models, see e.g., [4] and the references therein.
Then, the final linear parameter-varying (LPV) reformulation of the above LTV system reads
2 Acknowledgement & Origin
The base model was developed [5], [6] in the Collaborative Research Centre Transregio 96 Thermo-Energetic Design of Machine Tools funded by the Deutsche Forschungsgemeinschaft .
3 Data
3.1 Switched System Data
The data file VertStand_SLS.tar.gz contains the matrices
defining the subsystems of the switched linear system.
The matrices 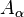 and
and 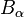 are numbered according to the slide position in descending order (1 - uppermost slide position / 11 - lowest slide position).
are numbered according to the slide position in descending order (1 - uppermost slide position / 11 - lowest slide position).
System dimensions:
3.2 Parametric System Data
The data file VertStand_PAR.tar.gz contains the matrices
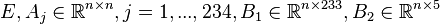 and
and 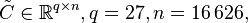
as well as a file ycoord_layers.mtx containing the y-coordinates of the layers located on the guide rails.
Here 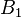 contains all columns corresponding to the different layers and
contains all columns corresponding to the different layers and 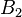 correlates to the boundaries where the external temperatures act on.
correlates to the boundaries where the external temperatures act on.
In order to set up the parameter dependent matrices 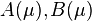 the active matrices
the active matrices  and columns
and columns 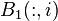 associated to the covered layers have to be identified via the current position of the tool slide and the y-coordinates of the different layers given in ycoord_layers.mtx. Then,
associated to the covered layers have to be identified via the current position of the tool slide and the y-coordinates of the different layers given in ycoord_layers.mtx. Then, 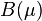 has to be set up in the form
has to be set up in the form ![B(\mu)=[\sum_{i\in id_{active}}\!\!\!\!\!B_1(:,i),B_2]](/morwiki/images/math/7/8/2/7820867bec5c0ae756abef1c30c2b6f6.png) . Similar to the switched systems approach, the layers are numbered in descending order.
. Similar to the switched systems approach, the layers are numbered in descending order.
4 Citation
To cite this benchmark, use the following references:
- For the benchmark itself and its data:
- The MORwiki Community, Vertical Stand. MORwiki - Model Order Reduction Wiki, 2018. http://modelreduction.org/index.php/Vertical_Stand
@MISC{morwiki_vertstand,
author = {{The MORwiki Community}},
title = {Vertical Stand},
howpublished = {{MORwiki} -- Model Order Reduction Wiki},
url = {http://modelreduction.org/index.php/Vertical_Stand},
year = 2014
}
- For the background on the benchmark:
@Article{morLanSB14,
author = {Lang, N. and Saak, J. and Benner, P.},
title = {Model Order Reduction for Systems with Moving Loads},
journal = {at-Automatisierungstechnik},
volume = 62,
number = 7,
pages = {512--522},
year = 2014,
doi = {10.1515/auto-2014-1095}
}
5 References
- ↑ N. Lang and J. Saak and P. Benner, Model Order Reduction for Systems with Moving Loads , in De Gruyter Oldenbourg: at-Automatisierungstechnik, Volume 62, Issue 7, Pages 512-522, 2014
- ↑ N. Lang, J. Saak and P. Benner, Model Order Reduction for Thermo-Elastic Assembly Group Models , In: Thermo Energetic Design of Machine Tools, Lecture Notes in Production Engineering, 85-92, 2015
- ↑ D. Liberzon, Switching in Systems and Control , Springer-Verlag, New York, 2003
- ↑ U. Baur, C. A. Beattie, P. Benner, and S. Gugercin, "Interpolatory projection methods for parameterized model reduction", SIAM J. Sci. Comput., 33(5):2489-2518, 2011
- ↑ A. Galant, K. Großmann, and A. Mühl, Model Order Reduction (MOR) for Thermo-Elastic Models of Frame Structural Components on Machine Tools. ANSYS Conference \& 29th CADFEM Users’ Meeting 2011, October 19-21, 2011, Stuttgart, Germany
- ↑ A. Galant, K. Großmann and A. Mühl, Thermo-Elastic Simulation of Entire Machine Tool , In: Thermo Energetic Design of Machine Tools, Lecture Notes in Production Engineering, 69-84, 2015