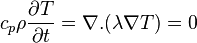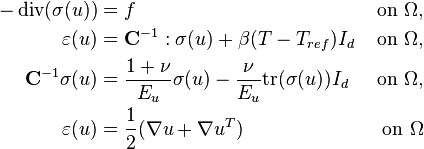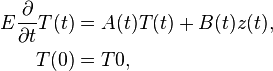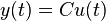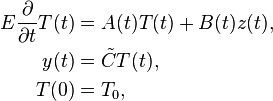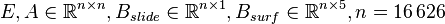| Line 52: | Line 52: | ||
===Discretized Model=== |
===Discretized Model=== |
||
The solid model has been generated and meshed in [[wikipedia:ANSYS|ANSYS]]. |
The solid model has been generated and meshed in [[wikipedia:ANSYS|ANSYS]]. |
||
| − | For the spatial discretization the [[wikipedia:finite element method|finite element method]] with linear Lagrange elements has been used and is implemented in [[wikipedia:FEniCS Project|FEniCS]]. The resulting system of [[wikipedia:ordinary differential equations|ordinary differential equations]] reads |
+ | For the spatial discretization the [[wikipedia:finite element method|finite element method]] with linear Lagrange elements has been used and is implemented in [[wikipedia:FEniCS Project|FEniCS]]. The resulting system of [[wikipedia:ordinary differential equations|ordinary differential equations (ODE)]], representing the thermal behavior of the stand, reads |
:<math> |
:<math> |
||
\begin{align} |
\begin{align} |
||
| − | E \frac{\partial}{\partial |
+ | E \frac{\partial}{\partial t} T(t) &= A(t)T(t) + B(t)z(t), \\ |
| − | + | T(0) &= T0, |
|
\end{align} |
\end{align} |
||
</math> |
</math> |
||
| − | with <math>t>0</math> and a system dimension of <math>n=16\,626</math> degrees of freedom and <math>m=6</math> inputs. Note that <math>A(.)\in\mathbb{R}^{n\times n}</math> and <math>B\in\mathbb{R}^{n\times m}</math> are time-dependent matrix-valued functions. More precisely, here the time dependence origins from the change of the boundary condition on <math>\Gamma_{slide}</math> due to the motion of the tool slide. The system input is given by |
+ | with <math>t>0</math> and a system dimension of <math>n=16\,626</math> degrees of freedom and <math>m=6</math> inputs. Note that <math>A(.)\in\mathbb{R}^{n\times n}</math> and <math>B\in\mathbb{R}^{n\times m}</math> are time-dependent matrix-valued functions. More precisely, here the time dependence origins from the change of the boundary condition on <math>\Gamma_{slide}</math> due to the motion of the tool slide. The system input is, according to the boundary conditions, given by |
:<math> |
:<math> |
||
z_i=\begin{cases} |
z_i=\begin{cases} |
||
| Line 68: | Line 68: | ||
\end{cases}. |
\end{cases}. |
||
</math> |
</math> |
||
| + | The discretized stationary elasticity model becomes |
||
| ⚫ | |||
:<math> |
:<math> |
||
| − | + | Mu(t)=KT(t). |
|
| + | </math> |
||
| ⚫ | |||
| + | :<math> |
||
| + | y(t) = C u(t) |
||
</math> |
</math> |
||
is given. |
is given. |
||
| + | Exploiting the one-sided coupling of the temperature and deformation fields, and reorganizing the elasticity equation in the form <math>u(t)=M^{-1}KT(t)</math>, the heat equation and the elasticity model can easily be combined in via the output equation. Finally, the thermo-elastic control system is of the form |
||
| − | |||
| + | :<math> |
||
| + | \begin{align} |
||
| + | E \frac{\partial}{\partial t} T(t) &= A(t)T(t) + B(t)z(t), \\ |
||
| + | y(t)& = \tilde{C}T(t),\\ |
||
| + | T(0) &= T_0, |
||
| + | \end{align} |
||
| + | </math> |
||
| + | where the modified output matrix <math>\tilde{C}=CM^{-1}KT(t)</math> includes the entire elasticity information. |
||
'''Geometrical dimensions:''' |
'''Geometrical dimensions:''' |
||
Revision as of 11:57, 15 March 2018
 Note: This page has not been verified by our editors.
Note: This page has not been verified by our editors.
1 Description
The vertical stand (see xx--CrossReference--dft--fig:cad--xx) represents a structural part of a machine tool. On one of its surfaces a pair of guide rails is located. Caused by a machining process a tool slide is moving on these rails. The machining process produces a certain amount of heat which is transported through the structure into the vertical stand. This heat source is considered to be a temperature input at the guide rails. The induced temperature field, denoted by  is modeled by the heat equation
is modeled by the heat equation
with the boundary conditions
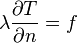 on
on 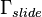 (surface where the tool slide is moving on the guide rails),
(surface where the tool slide is moving on the guide rails),
describing the heat transfer between the tool slide and the vertical stand. The heat transfer to the ambiance is given by the fixed Robin-type boundary condition
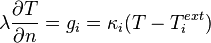 on
on  (remaining boundaries).
(remaining boundaries).
The motion driven temperature input and the associated change in the temperature field  lead to deformations
lead to deformations  within the stand structure.
Since the mechanical behavior of the machine stand is assumed to be much faster than the propagation of the thermal field, it is sufficient to consider the
stationary linear elasticity equations
within the stand structure.
Since the mechanical behavior of the machine stand is assumed to be much faster than the propagation of the thermal field, it is sufficient to consider the
stationary linear elasticity equations
1.1 Discretized Model
The solid model has been generated and meshed in ANSYS. For the spatial discretization the finite element method with linear Lagrange elements has been used and is implemented in FEniCS. The resulting system of ordinary differential equations (ODE), representing the thermal behavior of the stand, reads
with  and a system dimension of
and a system dimension of 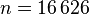 degrees of freedom and
degrees of freedom and 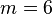 inputs. Note that
inputs. Note that 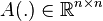 and
and 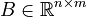 are time-dependent matrix-valued functions. More precisely, here the time dependence origins from the change of the boundary condition on
are time-dependent matrix-valued functions. More precisely, here the time dependence origins from the change of the boundary condition on 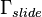 due to the motion of the tool slide. The system input is, according to the boundary conditions, given by
due to the motion of the tool slide. The system input is, according to the boundary conditions, given by
The discretized stationary elasticity model becomes
For the observation of the displacements in single points/regions of interest an output equation of the form
is given.
Exploiting the one-sided coupling of the temperature and deformation fields, and reorganizing the elasticity equation in the form 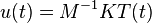 , the heat equation and the elasticity model can easily be combined in via the output equation. Finally, the thermo-elastic control system is of the form
, the heat equation and the elasticity model can easily be combined in via the output equation. Finally, the thermo-elastic control system is of the form
where the modified output matrix 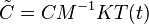 includes the entire elasticity information.
Geometrical dimensions:
includes the entire elasticity information.
Geometrical dimensions:
Stand: Width ( direction):
direction): 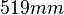 , Height (
, Height ( direction):
direction): 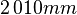 , Depth (
, Depth (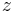 direction):
direction): 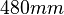
Guide rails: ![y\in [519, 2\,004] mm](/morwiki/images/math/d/6/6/d6623742beb91c8320ac3a3a6356fe02.png)
Slide: Height 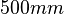
The heat load  induced by the slide and the external temperature
induced by the slide and the external temperature 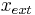 serve as the input
serve as the input  of the corresponding state-space system.
of the corresponding state-space system.
The motion of the tool slide and the associated variation of the affected input boundary are modeled by two different system representations. The following specific model representations have been developed and investigated in [1], [2].
1.2 Switched linear system
For the model description as a switched linear system, the guide rails of
the machine stand are modeled as 15 equally distributed horizontal
segments with a height of 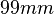 (see a schematic depiction in xx--CrossReference--dft--fig:segm--xx). Any of these segments
is assumed to be completely covered by the tool slide if its midpoint
(in y-direction) lies within the height of the slide. On the other
hand, each segment whose midpoint is not covered is treated as not in
contact and therefore the slide always covers exactly 5 segments at
each time. This in fact defines 11 distinct,
discrete boundary condition configurations for the stand model that are prescribed by the geometrical dimensions of the segmentation and the tool slide. These
distinguishable setups define the subsystems
(see a schematic depiction in xx--CrossReference--dft--fig:segm--xx). Any of these segments
is assumed to be completely covered by the tool slide if its midpoint
(in y-direction) lies within the height of the slide. On the other
hand, each segment whose midpoint is not covered is treated as not in
contact and therefore the slide always covers exactly 5 segments at
each time. This in fact defines 11 distinct,
discrete boundary condition configurations for the stand model that are prescribed by the geometrical dimensions of the segmentation and the tool slide. These
distinguishable setups define the subsystems
of the switched linear system [3], where 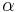 is a piecewise constant function of time, which takes
its value from the index set
is a piecewise constant function of time, which takes
its value from the index set 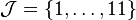 . To be more precise, the switching signal
. To be more precise, the switching signal 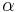 implicitly maps the slide position to the number of the currently active subsystem.
implicitly maps the slide position to the number of the currently active subsystem.
1.3 Linear Parameter-varying system
2 Acknowledgement & Origin
The base model was developed [4], [5] in the Collaborative Research Centre Transregio 96 Thermo-Energetic Design of Machine Tools funded by the Deutsche Forschungsgemeinschaft .
3 Data
3.1 Switched System Data
3.2 Parametric System Data
The data file Data_VertStand.tar.gz contains a MAT_File matrices.mat which consists of the matrices
in sparse format and a file with the coordinates of the mesh nodes called coord.txt.
Here 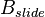 consists of all nodes located on the guide rails.
consists of all nodes located on the guide rails.
In order to get a parameter dependent matrix
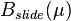 one has to pick the "active" nodes (nodes hit by tool carriage) at vertical position
one has to pick the "active" nodes (nodes hit by tool carriage) at vertical position 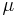 .
The "active" nodes are in the interval of
.
The "active" nodes are in the interval of ![[\mu-\frac{d}{2},\mu+\frac{d}{2}]](/morwiki/images/math/a/7/1/a71f92fd4be99066106491025fe32ad6.png) , where
, where 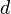 is the heigth of the slide.
is the heigth of the slide.
The file coord.txt provided in Data_VertStand.tar.gz includes a column with indices followed by three additional columns containing the spatial coordinates 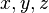 of the corresponding nodes.
of the corresponding nodes.
The matrix 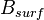 describes the locations where the external temperatures act on.
The first column is responsible for the input of the temperature at the clamped bottom slice of the structure.
Column 2 describes the ... part of the stand. Columns 3 to 5 describe different thresholds with respect to the height of ambient air temperature.
The third column includes the nodes of the lower third
describes the locations where the external temperatures act on.
The first column is responsible for the input of the temperature at the clamped bottom slice of the structure.
Column 2 describes the ... part of the stand. Columns 3 to 5 describe different thresholds with respect to the height of ambient air temperature.
The third column includes the nodes of the lower third  of the stand.
In column 4 all nodes of the middle third
of the stand.
In column 4 all nodes of the middle third 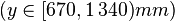 of the geometry are contained
and the fifth column of
of the geometry are contained
and the fifth column of 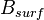 includes the missing upper
includes the missing upper ![(y\in[1\,340,2\,010]mm)](/morwiki/images/math/8/f/7/8f7ee61fb31ab9462369fff516b9d051.png) part.
part.
4 Citation
To cite this benchmark, use the following references:
- For the benchmark itself and its data:
- The MORwiki Community. Vertical Stand. MORwiki - Model Order Reduction Wiki, 2018. http://modelreduction.org/index.php/Vertical_Stand
@MISC{morwiki_vertstand,
author = {The {MORwiki} Community},
title = {Vertical Stand},
howpublished = {{MORwiki} -- Model Order Reduction Wiki},
url = {http://modelreduction.org/index.php/Vertical_Stand},
year = {2014}
}
- For the background on the benchmark:
@Article{morLanSB14,
author = {Lang, Norman and Saak, Jens and Benner, Peter},
title = {Model Order Reduction for Systems with Moving Loads},
journal = {at-Automatisierungstechnik},
year = 2014,
volume = 62,
number = 7,
pages = {512--522},
month = {June},
publisher = {deGruyter},
doi = {10.1515/auto-2014-1095}
}
5 References
- ↑ N. Lang and J. Saak and P. Benner, Model Order Reduction for Systems with Moving Loads , in De Gruyter Oldenbourg: at-Automatisierungstechnik, Volume 62, Issue 7, Pages 512-522, 2014
- ↑ N. Lang, J. Saak and P. Benner, Model Order Reduction for Thermo-Elastic Assembly Group Models , In: Thermo Energetic Design of Machine Tools, Lecture Notes in Production Engineering, 85-92, 2015
- ↑ D. Liberzon, Switching in Systems and Control , Springer-Verlag, New York, 2003
- ↑ A. Galant, K. Großmann, and A. Mühl, Model Order Reduction (MOR) for Thermo-Elastic Models of Frame Structural Components on Machine Tools. \textit{ANSYS Conference \& 29th CADFEM Users’ Meeting 2011, October 19-21, 2011, Stuttgart, Germany
- ↑ A. Galant, K. Großmann and A. Mühl, Thermo-Elastic Simulation of Entire Machine Tool , In: Thermo Energetic Design of Machine Tools, Lecture Notes in Production Engineering, 69-84, 2015