| Line 36: | Line 36: | ||
with the fluid velocity <math>p(=v) \in [0, 1]</math> as single parameter. |
with the fluid velocity <math>p(=v) \in [0, 1]</math> as single parameter. |
||
| − | Here <math>E</math> is the heat capacitance matrix, <math>b</math> is the load vector which is derived from separating the spatial and temporal variables in <math>\dot{q}</math> and the FEM discretization w.r.t. the spatial variables. <math> |
+ | Here <math>E</math> is the heat capacitance matrix, <math>b</math> is the load vector which is derived from separating the spatial and temporal variables in <math>\dot{q}</math> and the FEM discretization w.r.t. the spatial variables. <math>A_i</math> are the stiffness matrices with <math>i=v0</math> for pure diffusion and <math>i=v1</math> for diffusion and convection. Thus, for obtaining pure convection you have to compute <math>A_{v1} - A_{v0}</math>. |
Example with 3 parameters: |
Example with 3 parameters: |
||
| − | Here, all fluid properties |
+ | Here, all fluid properties are identified as parameters. Thus, we consider the following transfer function |
<math> |
<math> |
||
Revision as of 17:40, 28 November 2011
Description
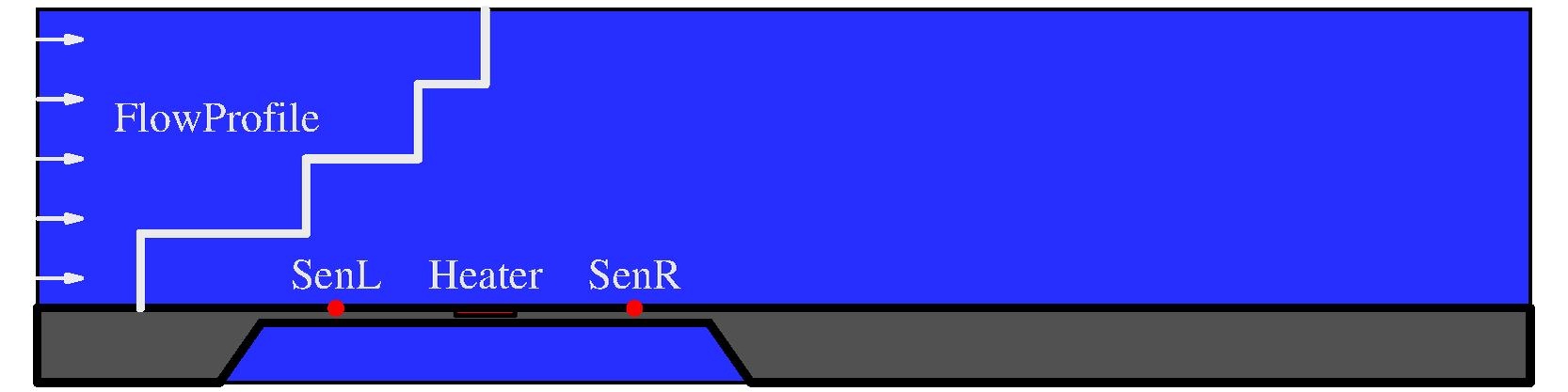
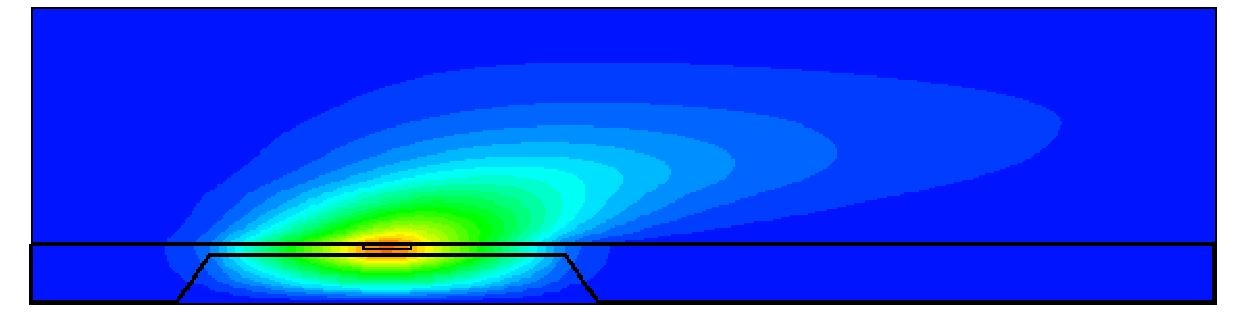
An anemometer is a flow sensing device, consisting of a heater and temperature sensors before and after the heater, placed either directly in the flow or in its vicinity. They are located on a membrane to minimize heat dissipation through the structure. Without any flow, the heat dissipates symmetrically into the fluid. This symmetry is disturbed if a flow is applied to the fluid, which leads to a convection on the temperature field and therefore to a difference between the temperature sensors (see Fig.1 below) from which the fluid velocity can be determined.
The physical model can be expressed by the convection-diffusion partial differential equation [4]\[\rho c \frac{\partial T}{\partial t} = \nabla \cdot (\kappa \nabla T ) - \rho c v \nabla T + \dot q,\]
where \(\rho\) denotes the mass density, \(c\) is the specific heat, \(\kappa\) is the thermal conductivity, \(v\) is the fluid velocity, \(T\) is the temperature, and \(\dot q\) is the heat flow into the system caused by the heater.
The solid model has been generated and meshed in ANSYS. Triangular PLANE55 elements have been used for the finite element discretization. The order of the system is \(n = 29008\).
Example with 1 parameter:
The \(n\) dimensional ODE system has the following transfer function \( G(p) = c((sE - A_{v0}- p(A_{v1} - A_{v0}))^{-1}b) \)
with the fluid velocity \(p(=v) \in [0, 1]\) as single parameter. Here \(E\) is the heat capacitance matrix, \(b\) is the load vector which is derived from separating the spatial and temporal variables in \(\dot{q}\) and the FEM discretization w.r.t. the spatial variables. \(A_i\) are the stiffness matrices with \(i=v0\) for pure diffusion and \(i=v1\) for diffusion and convection. Thus, for obtaining pure convection you have to compute \(A_{v1} - A_{v0}\).
Example with 3 parameters:
Here, all fluid properties are identified as parameters. Thus, we consider the following transfer function
\( G(p_0,p_1,p_2) = c((s \underbrace{(M_s + p_0 M_f)}_{E(p_0)} - \underbrace{( A_{d,s} + p_1 A_{d,f} + p_2 A_c )}_{A(p_1,p_2)} )^{-1}b) \)
with parameters \(p_0 \in [0, 1], p_1\in [0.1, 2], p_2 \in [1, 2]\) which are combination of the original fluid parameters \(\rho, c, \kappa, \vec v: p_0 = \rho c, p_1=\kappa\) and \(p_2 =\rho c v\), see [5].
Provenance
IMTEK Freiburg, group of Jan Korvink
Data information
Matrices are in the Matrix Market format(http://math.nist.gov/MatrixMarket/), and can be downloaded here, data for the example with one parameter: File:Matrices 1d.tar.gz, and data for the example with three parameter: File:Matrices 3d.tgz. The matrix name is used as an extension of the matrix file. The system matrices have been extracted from ANSYS models by means of mor4fem. For more information about permutation, computing the matrices, output, look into readme.txt.
Example with 1 parameter:
- .B: load vector
- .E: damping matrix
- .C: permutation matrix
- .A: stiffness matrices
\(\_v0\): diffusion \(\_v1\): diffusion and convection
Example with 3 parameters:
- .B: load vector
- .E: damping matrices (2)
- .A: stiffness matrices (5)
Related paper
a) About the anemometer}
[1] H. Ernst,"High-Resolution Thermal Measurements in Fluids," PhD thesis, University of Freiburg, Germany(2001).
[2] P. Benner, V. Mehrmann and D. Sorensen, "Dimension Reduction of Large-Scale Systems," Lecture Notes in Computational Science and Engineering, Springer-Verlag, Berlin/Heidelberg, Germany, 45, 2005.
[3] C. Moosmann and A. Greiner, "Convective Thermal Flow Problems," Chapter 16 (pages 341--343) of [2].
b) MOR for non-parametrized anemometer}
[4] C. Moosmann, E. B. Rudnyi, A. Greiner and J. G. Korvink, "Model Order Reduction for Linear Convective Thermal Flow," Proceedings of 10th International Workshops on THERMal INvestigations of ICs and Systems, THERMINIC2004, 29 Sept - 1 Oct, 2004, Sophia Antipolis, France.
c) MOR for parametrized anemometer}
[5] U.~Baur, P.~Benner, A.~Greiner, J.~G. Korvink, J.~Lienemann and C.~Moosmann, "Parameter preserving model order reduction for {MEMS} applications," MCMDS Mathematical and Computer Modelling of Dynamical Systems, 17(4):297--317, 2011.
[6] C. Moosmann, "ParaMOR - Model Order Reduction for parameterized MEMS applications," PhD thesis, University of Freiburg, Germany(2007).
[7] C. Moosmann, E. B. Rudnyi, A. Greiner, J. G. Korvink and M. Hornung," Model Order Reduction of a Flow Meter," Technical Proceedings of the 2005 Nanotechnology Conference and Trade Show, Nanotech 2005, May 8-12, 2005, Anaheim, California, USA, NSTINanotech 2005, vol. 3, p. 684-687.
[8] E. B. Rudnyi, C. Moosmann, A. Greiner, T. Bechtold, J. G. Korvink, "Parameter Preserving
Model Reduction for MEMS System-level Simulation and Design," Proceedings of MATHMOD 2006}, February 8 -
10, 2006, Vienna University of Technology, Austria.
Fig. 1 2d-model-anemometer