Difference between revisions of "Balanced Truncation"

Revision as of 09:44, 25 March 2013

An important projection model reduction method which delivers high quality reduced models by making an extra effort in choosing the projection subspaces.

A stable system 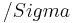$/Sigma$ , realized by (A,B,C,D) is called balanced, if the Gramians, i.e. the solutions P,Q of the Lyapunov equations

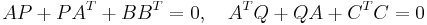
$AP+PA^T+BB^T=0,\quad A^TQ+QA+C^TC=0$

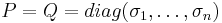satisfy $P=Q=diag(\sigma_1,\dots,\sigma_n)$ with $\sigma_1\geq\sigma_2\geq \dots\geq\sigma_n\geq0$

References

@@ Line 4: / Line 4: @@
-A stable system </math>Sigma<math>
+A stable system <math>/Sigma</math> , realized by (A,B,C,D) is called balanced, if the Gramians, i.e. the solutions P,Q  of the Lyapunov equations
+<math> AP+PA^T+BB^T=0,\quad A^TQ+QA+C^TC=0</math>
+satisfy <math> P=Q=diag(\sigma_1,\dots,\sigma_n)</math> with <math> \sigma_1\geq\sigma_2\geq \dots\geq\sigma_n\geq0</math>
 ==References==