(Created page with ' These methods are very efficient in many engineering applications, including circuit simulation, where the robustness of the methods were originally found. Methods based on …') |
|||
| Line 1: | Line 1: | ||
| + | [[Category:method]] |
||
| + | The moment-matching methods are also called the Krylov subspace methods, as well as |
||
| + | Pad<math>\'e</math> approximation methods. These methods are applicable for non-parametric linear time invariant systems, often the descriptor systems, e.g. |
||
| + | <math>Insert formula here</math> |
||
| ⚫ | |||
| − | |||
| ⚫ | |||
| − | Methods based on Krylov subspaces are often designed for a direct application to descriptor systems~(\ref{descriptor}). |
||
| − | In order to be in agreement with the previous section, we describe the methods for the application to the standard state space system in~(\ref{e2.4}). |
||
The basic steps are as follows. First, the transfer function~(\ref{eq:TFM}) is expanded into a power series at an expansion point $s_0\in\mathbb{C}\cup \infty$. |
The basic steps are as follows. First, the transfer function~(\ref{eq:TFM}) is expanded into a power series at an expansion point $s_0\in\mathbb{C}\cup \infty$. |
||
Revision as of 09:42, 13 March 2013
The moment-matching methods are also called the Krylov subspace methods, as well as
PadFailed to parse (lexing error): \'e
approximation methods. These methods are applicable for non-parametric linear time invariant systems, often the descriptor systems, e.g.
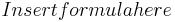
They are very efficient in many engineering applications, including circuit simulation, where the robustness of the methods were originally found.
The basic steps are as follows. First, the transfer function~(\ref{eq:TFM}) is expanded into a power series at an expansion point $s_0\in\mathbb{C}\cup \infty$. % % Let $s=s_0+\sigma$, then, within the convergence radius of the series, we have \[ \begin{array}{lll} &&H(s_0 + \sigma)= L^T[(s_{0}+\sigma){I}-A]^{-1}B \\ &&=L^T[\sigma { I}+(s_{0}{ I}-{ A})]^{-1}B\\ &&=L^T[{ I}-\sigma(s_0{ I}-{ A})^{-1}]^{-1}[-(s_0{ I}-{ A})]^{-1}B\\ &&=L^T[{ I}+\sigma(s_0{ I}- A )^{-1}+\sigma^2[(s_0{ I}-{ A})^{-1}]^{2}+\ldots]\times\\ &&\quad({ A}-s_0{I})^{-1}B\\ &&=\sum \limits^\infty_{i=0}\underbrace{L^T[(s_0{ I}-{A})^{-1}]^i({ A}-s_0{ I})^{-1}B}_{:= m_i(s_0)} \, \sigma^i, \end{array} \] % % where $m_i(s_0)$ are called the moments of the transfer function about $s_0$ for $i=0,1,2,\ldots$. If the expansion point is chosen as zero then the moments simplify to $m_i(0)=L^\mathrm{T}(-A^{-1})^{i+1}B$. For $s_0=\infty$ the moments are also called Markov parameters which can be computed by $L^\mathrm{T} \bA^{i-1}B$.
The goal in moment-matching model reduction is the construction of a reduced order system where some moments $\hat m_i$ of the associated transfer function $\hat H$ match some moments of the original transfer function $H$. A few important classes of approximations are listed in Table~\ref{tab:moments}. % % \begin{center} \begin{table*}[ht] \hfill{} \begin{tabular}{l|ll} %\hline Name of reduced order system& Matched moments &\\\hline %\cline{3-4} %\hline Pad\'e approximation~\cite{Bak75} & $m_i(s_0) = \hat m_i(s_0)$, & $i=0,1,\cdots,2r-1$ \\ Partial realization~\cite{GraL83} & $m_i(\infty) = \hat m_i(\infty)$, & $i=0,1,\cdots,2r-1$ \\ Multipoint Pad\'e approximation or & $m_i(s_j) = \hat m_i(s_j)$, & $i=0,1,\cdots,2r_j-1$, for $j=1,\cdots,k$, and $r_1+\dots+r_k = r$ \\ rational interpolation~\cite{AndA90,Bak75} & & %\hline \end{tabular} \hfill{} \caption{Some examples for model reduction by moment-matching.} \label{tab:moments} \end{table*} \end{center}
