| Line 87: | Line 87: | ||
But more attention should be paid for the dynamics of the system and the stability is also a major concern, |
But more attention should be paid for the dynamics of the system and the stability is also a major concern, |
||
especially for the nonlinear case. Mostly, we use the same notation as time-independent case except the |
especially for the nonlinear case. Mostly, we use the same notation as time-independent case except the |
||
| − | variable <math> t < |
+ | variable <math> t </math> is added explicitly. |
The exact, infinite-dimensional formulation, indicated by the superscript e, is given by |
The exact, infinite-dimensional formulation, indicated by the superscript e, is given by |
||
Revision as of 17:15, 19 November 2012
The Reduced Basis Method (RBM) we present here is applicable to static and time-dependent linear PDEs.
Time-Independent PDEs
The typical model problem of the RBM consists of a parametrized PDE stated in weak form with
bilinear form 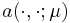 and linear form
and linear form 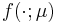 .
The parameter
.
The parameter 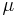 is considered within a domain
is considered within a domain 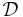 and we are interested in an output quantity
and we are interested in an output quantity 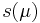 which can be
expressed via a linear functional of the field variable
which can be
expressed via a linear functional of the field variable 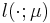 .
.
The exact, infinite-dimensional formulation, indicated by the superscript e, is given by
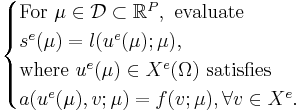
We assume a large-scale discretization to be given, such that we consider
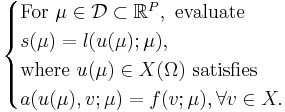
The underlying assumption of the RBM is that the parametrically induced manifold 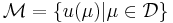 can be approximated by a low dimensional space
can be approximated by a low dimensional space 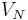 .
.
It also applies the concept of an offline-online decomposition, in that a large pre-processing offline cost is acceptable in view of a very low online cost (of a reduced order model) for each input-output evaluation, when in a many-query or real-time context.
The essential assumption which allows the offline-online decomposition is that there exists an affine parameter dependence
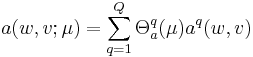
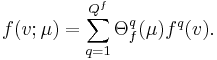
The Lagrange Reduced Basis space is established by iteratively choosing Lagrange parameter samples
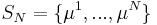
and considering the associated Lagrange RB spaces
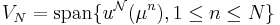
in a greedy sampling. This leads to hierarchical RB spaces: 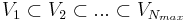 .
.
We then consider the galerkin projection onto the RB-space 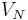
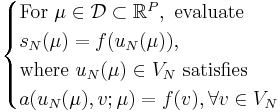
The greedy sampling uses an error estimator 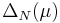 which estimates (even rigorously, in some cases) the approximation error
which estimates (even rigorously, in some cases) the approximation error 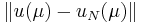 .
.
Let  denote a finite sample of
denote a finite sample of 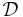 and set
and set 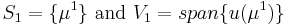 .
For
.
For 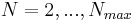 , find
, find 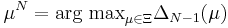 ,
and then set
,
and then set 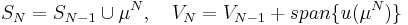 .
.
Time-Dependent PDEs
When time is involved, it can be roughly considered as an usual parameter just as time-independent problems.
But more attention should be paid for the dynamics of the system and the stability is also a major concern,
especially for the nonlinear case. Mostly, we use the same notation as time-independent case except the
variable 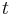 is added explicitly.
is added explicitly.
The exact, infinite-dimensional formulation, indicated by the superscript e, is given by
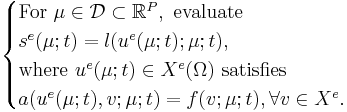
References
G. Rozza, D.B.P. Huynh, A.T. Patera Reduced Basis Approximation and a Posteriori Error Estimation for Affinely Parametrized Elliptic Coercive Partial Differential Equations, Arch Comput Methods Eng (2008) 15: 229–275
Contact information:
